Midterm Cheat Sheet
|
Linear Regression Predicting a CI new obs adds a 1 to se(y): |
Multiple Linear Regression and Estimation 𝐻0 : 𝛽1 = 𝛽2 = 𝛽3 = ⋯ = 𝛽𝑝 = 0 rejection rule of 𝑡 >= t(1 − alpha/2; 𝑛 − 𝑝 − 1) |
|
Model Fitting: Inference dfΩ = n - p, and df𝜔 = n – q Reject the null hypothesis if F > Fα p - q, n – p |
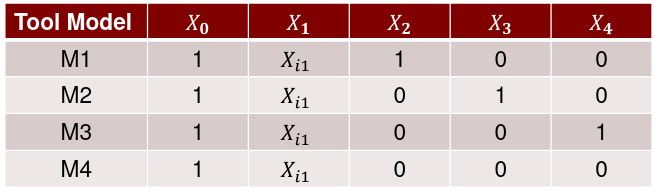
Dummy Variables and Analysis of Covariance An interaction between Xi1 and Xi2: A model with multiple categorical variables: |
|
Regression Diagnostics The Hat Matrix – n*n matrix
Calculate the t-test and compare abs with limit: |
Influential Points: causes changes to regression with a threshold of Where p’ is the number of parameters Cook's Distance: with a threshold of Error: a plot of e_hat should Shapiro-Wilk normality test H0: Residuals are normally distributed Bonferroni Correction: Divide alpha by n |
|
Variable Selection Backwards Elimination:
Cutoff p significance can be 15-20% for testing Forward Selection:
Stepwise regression: A combination of the two |
Selection Criteria: Mallow’s Cp Statistic: Avg MSE of prediction We desire models with small p and Cp around or less than p |
R Code Snippets
|
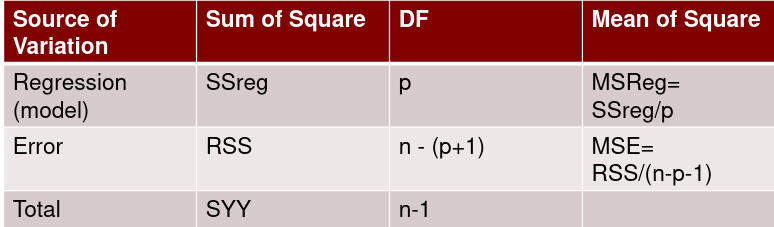
# Model with only beta_0 sr_lm0 <- lm(y ~ 1, data=sr) # Full model sr_lm1 <- lm(y ~ ., data=sr) sr_syy <- sum((savings$sr - mean(savings$sr))^2) sr_rss <- deviance(sr_lm1) # F = ((SYY -RSS)/((n-1) - (n-2))) / (RSS / (n - 1)) sr_num <- (sr_syy - sr_rss)/(df.residual(sr_lm0) - df.residual(sr_lm1)) sr_den <- sr_rss / df.residual(sr_lm1) sr_f <- sr_num / sr_den # dfΩ = n - p, and df𝜔 = n - q pf(sr_f, df.residual(sr_lm0) - df.residual(sr_lm1), df.residual(sr_lm1), lower.tail = F) # β=(XI X)−1 XIY beta <- solve(t(x)%*%x)%*%(t(x)%*%y) # Pearson's cor(lin_reg$fitted.values, lin_reg$residuals, method="pearson") # Stratify variables by a factor by(depress, depress$publicassist, summary) # Welsh's Two Sample T-test # For difference in means t.test(assist$cesd, noassist$cesd) # or t.test(data.y ~ factor) # CI of LS means based on covariates library(lsmeans) lsmeans(reg, ~Type) # Apply a mean function to an array # split on a factor tapply(assist$cesd, assist$assist, mean) # When a regression factor has # more than two categories reg <- lm(Pulse1 ~ Height + Sex + Smokes + as.factor(Exercise)) |
# Cook's Distance cook <- cooks.distance(reg) cook[cook > 4/n] # Shapiro Test for normallity shapiro.test(reg$residuals) # Studentized residuals stud <- rstudent(reg) # Threshold for lower tail of # studentized resids with correction lim = abs(qt(.05/(n*2), df = n - pprime - 1, lower.tail = T)) stud[which(abs(stud) > lim)] # Hat values hat <- hatvalues(reg) lev <- 2 * pprime / n hat[hat > lev] # Forward selection forward <- ~ year + unemployed + femlab + marriage + birth + military m0 <- lm(divorce ~ 1, data = usa) reg.forward.AIC <- step(m0, scope = forward, direction = "forward", k = 2) n <- nrow(usa) # AIC = n*log(RSS/n) + 2p' n*log(162.1228/n)+2*6 extractAIC(reg.forward.AIC, k=2) # BIC reg.forward.BIC <- step(m0, scope = forward, direction = "forward", k = log(n)) extractAIC(reg.forward,k=log(n)) # BIC = n*log(RSS/n) + p'*log*n) n*log(162.1228/n)+6*log(n) library(leaps) leaps <- regsubsets(divorce ~ .) rs <- summary(leaps) par(mfrow=c(1,2)) plot(2:7, rs$cp, xlab="No. of parameters", ylab="Cp Statistic") abline(0,1) |

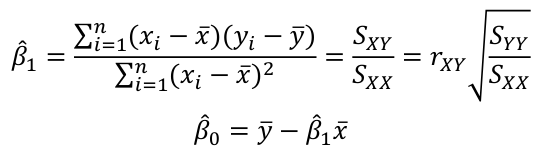
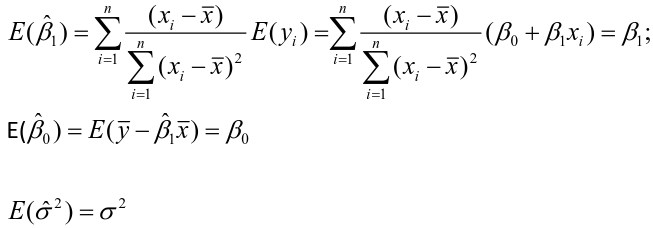
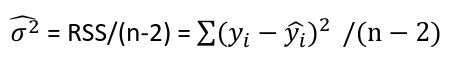
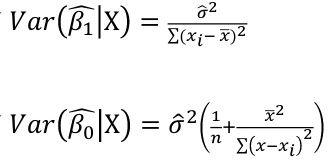
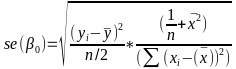
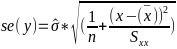
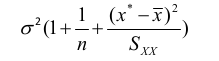
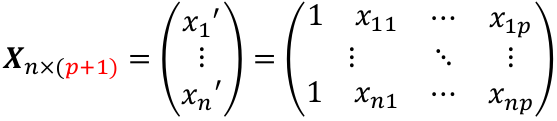
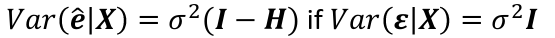
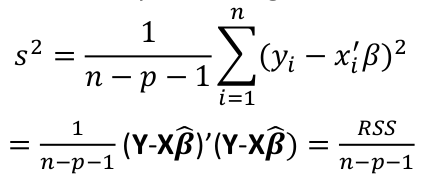
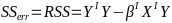
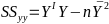
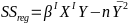
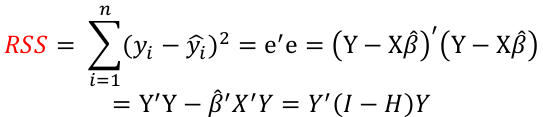
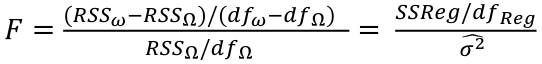
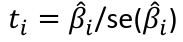
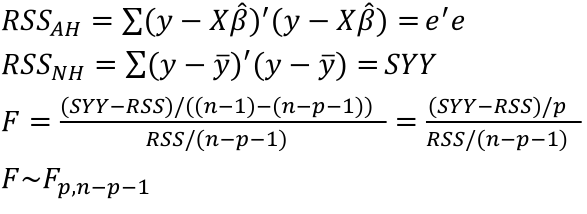
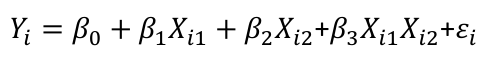
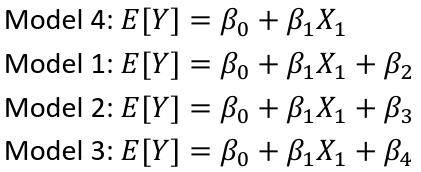
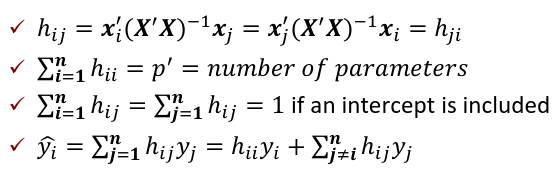
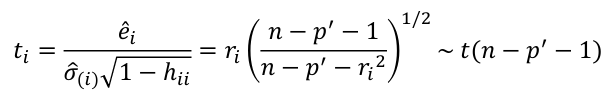
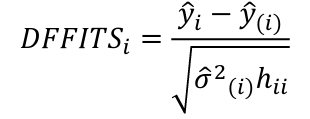
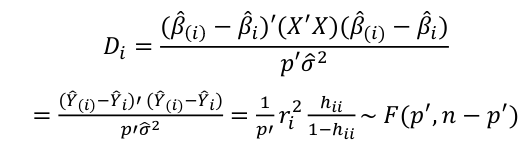

No Comments