Broken Stick Regression, Polynomial Regression, Splines
Transformations of the response and predictors can improve the fit and correct violations of model assumptions such as non-constant error variance. This chapter focuses on the transformation of predictors.
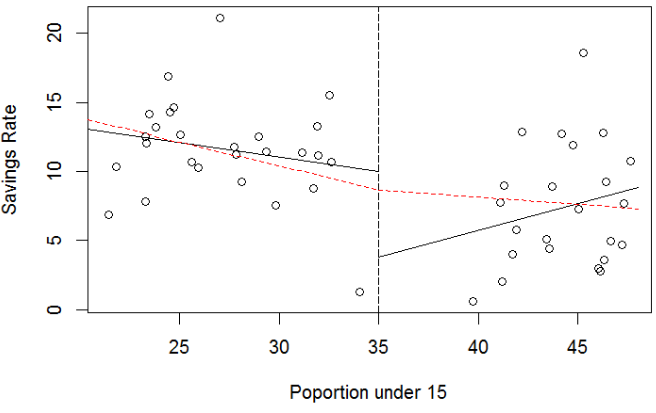
The idea behind Broken Stick Regression/Segmented Regression is that different linear regression models may apply in different regions of the data. We define two basis functions:
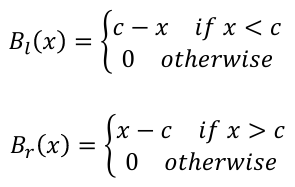
where c marks the division between groups. Bl(x) and Br(x) form a first-order spline basis with knot point c. Sometimes Bl(x) and Br(x) are called hockey-stick functions.
Polynomial Regression
Polynomial Regression models are frequently used curvilinear response models in practice. They make it easy to handle special cases of the linear regression model, however in reality this is not an exact representation.
We choose d by adding terms until the added term is not statistically significant. Start with a large d and eliminate non-statistically significant terms starting with the highest order term.
Regression Splines
- Polynomials regression has:
- the advantage of smoothness
- the disadvantage that each data point affects the fit globally
- Broken stick regression method
- Localized the influence of each data point to its particular segment
- Do not have the same smoothness as with polynomials
- Use B-spline basis functions
- Have both smoothness and local influence
- Can overfit the model

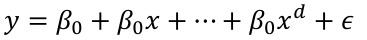
No Comments