Power and Sample Size Calculations for Association Studies
Review of errors and difference in means/proportions:
Type II error is represented by beta and type I error as alpha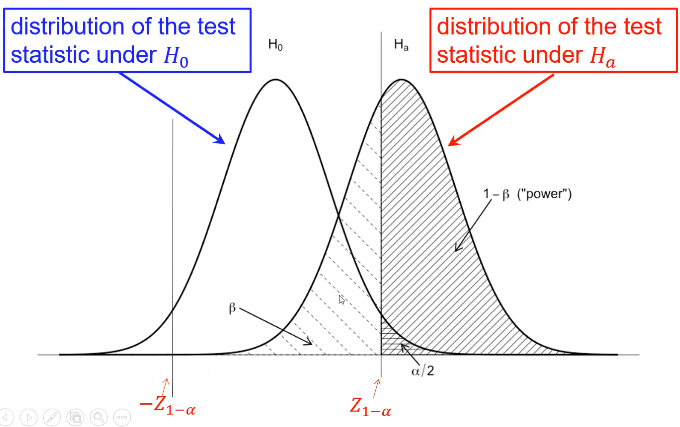
Where Z1 - (alpha /2)is the Z-value that creates the target value of alpha in the tail of the distribution. Power decreases as alpha increases.
Power also has a direct relationship with sample size. Sometimes we choose sample sized based on the desired power for a specific alternative hypothesis of interest, and other times we used a fixed sample size and significance level.
A Z-test of differences in proportions with 2 groups with different sample sizes: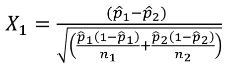
C is the mean of the distribution under the alternative hypothesis: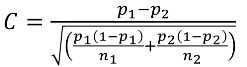
And the power can be calculated by taking the cdf of C minus the one sided Z-value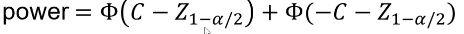
Likewise, we can use a similar z-test for differences in the mean of a quantitative trait: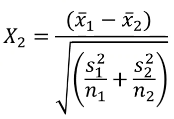
And the power can be calculated the same way as proportions.
Applying Power to Genetic Associations
- Difference in proportions: we can compute the power for a test that compares the allele or genotype frequency between cases and controls
- Difference in means: we can compare the mean trait values between individuals with different genotypes at a marker (and we can extend this to an F-test for a linear regression)
Dichotomous Traits
- Determine the expected genotype frequencies in cases and controls under the alternative hypothesis of interest
- Estimate power for given sample size or estimate minimum sample size required for given power and significance level under the planner analysis model
Genetic Model
- We usually use 4 parameters to specify the disease model for a dichotomous trait:
- Genotype relative risks y1 and y2
- Population prevalence of disease K
- Risk allele frequency q (the allele that increases risk of disease)
- To compute power, we need the genotype frequencies for cases and controls under the alternative hypothesis
- P(personal carries i risk alleles | affected)
- P(Person carries i risk alleles | unaffected)
- for i = 0,1, and 2
Genotype Relative Risk
Another way to parameterize penetrance, the probability that someone is affected given their genotype.
Penetrance fi = P(affected | i risk alleles) for i = 0,1, or 2 risk alleles at a locus
- f = (f0, f1, f2) is the penetrance for the genetic variant.
- f0 = f1 = f2 if there is no difference in probability of being affected by genotype -> the genotypes at this variant are not associated with case status
- If at least one fi != fj -> the genotype at this variant are associated with case status
- The genotype relative risks (GRR) are ratios of the penetrance values
- yi is the ratio of probabilities of being a case for someone with i risk alleles compared to someone with 0 risk alleles
- y1 = f1/f0
- y2 = f2/f0
- y1 = y2 = 1 -> f0 = f1 = f2 -> No difference in probability of being a case between genotypes with 1 or 2 risk allele(s) and 0 risk alleles -> no association between case status and genotype
So if we know the relative risks (y1 and y2), the population prevalence K, and the risk allele frequency q, we can determine the penetrances (f0, f1, f2):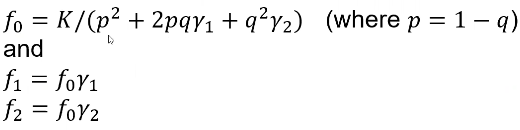
This is derived from the law of total probabilities which I will not show here.
Models for Dichotomous Traits
Note: multiplicative GRR ~= multiplicative OR
additive log(OR) -> multiplicative OR
Thus, multiplicative GRR model is most similar to the additive log(OR) model that we use in logistic regression
H0: Genotype or allele frequencies are the same in cases and controls
Ha: genotype frequencies are not equal in cases and controls. They follow a [dominant, recessive, additive] model
To compute power we need the genotype frequencies for the cases and controls under the alternative hypothesis:
P(i risk alleles | person is a case)
P(i risk alleles | person is a control)
For i = 0,1,2
The expected genotype frequencies for cases and control from f using Bayes Rule: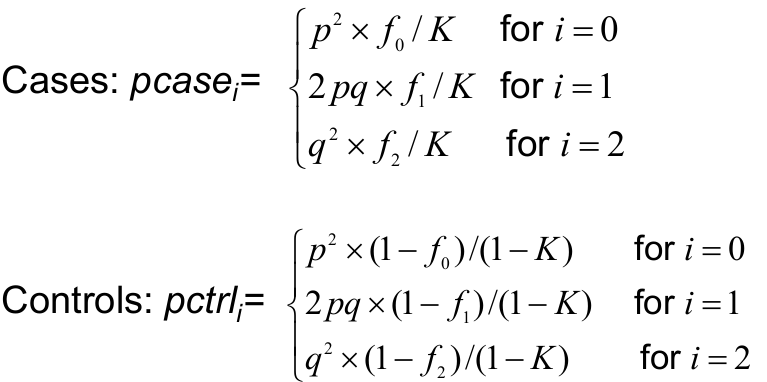
To compute power we not only have to specify the alternative hypothesis model, but also choose the model you will use to do the analysis. The analysis model is the model you choose for the analysis for which you compute power.
Under a dominant model the genotype relative risk should be y1 = y2 = 2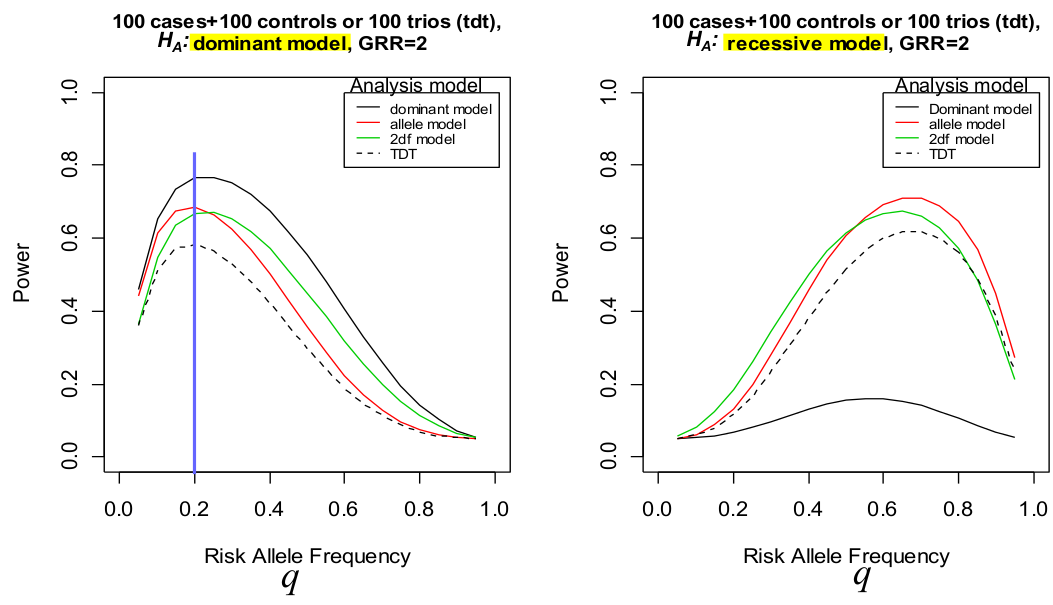
Notice how when we analyze the recessive model as a dominant one (right), the power decreases significantly.
Power - General 2DF Test
We can also compute power for the 2df genotype-based chi-squared test. The underlying formulas will not be explained here as there is software to compute this called the Genetic Power Calculator; You specify GRRs, prevalence risk allele frequency and it produces the genotype frequencies in cases and controls and the power under dominant, recessive, additive and 2DF tests.
Summary - Power for Dichotomous Traits
- Determine the expected genotype frequencies in cases and controls under the alternative hypothesis
- Need to specify genetic model/effect size
- Estimate power for given sample size or estimate minimum sample size required for given power using the specific analysis model and significance level
- Can also find the minimum effect size that yields specific (usually 80%) power for a given sample size and allele frequency
Quantitative Traits
We usually parameterize power for quantitative traits in terms of locus-specific heritability (h2), the proportion of variance explained by the genetic variant (R2). It is independent of underlying model and allele frequency.
For a linear regression F test, the power is determined by the non-centrality parameter 𝜆, the proportion of variance in the trait explained by the genotype (h2) * sample size
𝜆 = h2 * N
To determine the (central) F distribution:
In R: qf(1-alpha, df1, df2)
Code to determine power using non-central F-distribution and non-centrality parameter "ncp":
In R: pf(crit.val, df1, df2, ncp, lower.tail = F)
So for any proportion of variance explained by h2 and N we can compute power. However, a single h2 value corresponds to many alternative hypothesis models.
For dichotomous traits we can simply compute power for difference in proportions, but specifying an underlying genetic model (GRRs, prevalence, allele frequency) is more meaningful. Similarly, power for a quantitative trait is usually more meaningful if we understand how the heritability relates to the genotypic means for a trait -- the genetic model. To find this we need allele frequency for that allele that increases phenotype and the degree of dominance d (additive, dominant or recessive).
Genotypic Means
a is effect size
Recall the variance components in a single gene model:
Locus-specific heritability h2, degree of dominance d, and allele frequency p: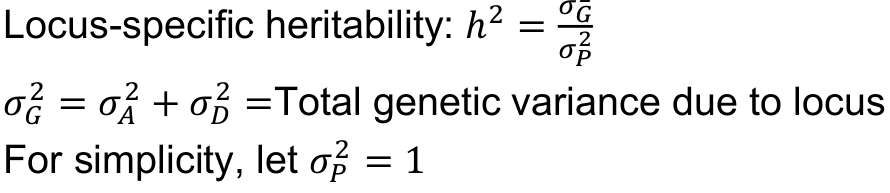
We can re-scale so that the total trait σ2P = 1, by dividing the trait values by SD: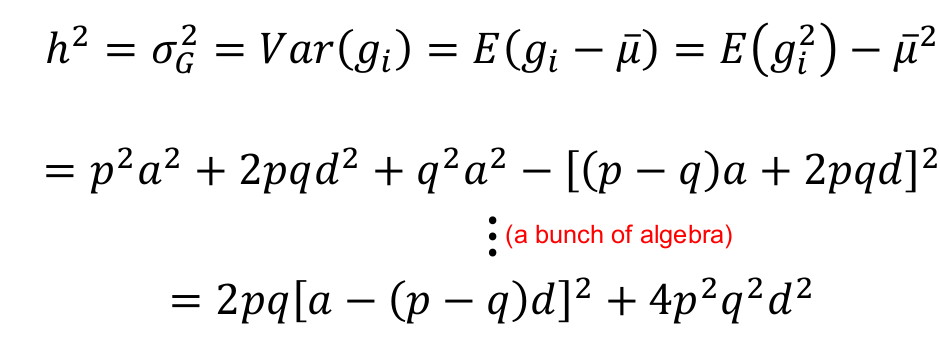
Next we can set R = (-1, 0, 1) for recessive, additive and dominant models respectively, then d = Ra. We substitute Ra for d in the above and solve for a: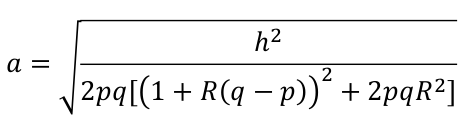
When R = 0: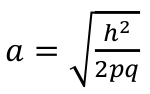
Recap on Effects on Power
- Dichotomous Traits (difference in proportions) are effected by:
- Effect size: Model (dom/rec/add...)
- GRRs
- Risk allele frequency
- Prevalence of disease/distribution of phenotype
- Quantitatice Trait
- Effect size: Proportion of variance explained by the genetic variant is affected by:
- Model (dom/rec/add...)
- Allele frequency
- Effect size: Proportion of variance explained by the genetic variant is affected by:
Use a significance level you will use when performing association tests, or the entire family-wise error for the entire experiment.
For the model, if there is no prior hypothesis, try to find examples from the literature of reasonable effect sizes for your alternative hypothesis. Usually under an additive or multiplicative model. Beware that differences in study design can lead to different expected effect sizes.
Winner's curse is when significant regression estimates from small underpowered samples are biased -- tend to over-estimate the true effect.

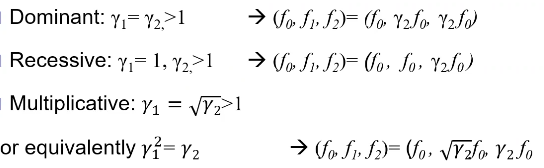
No Comments