Haplotypes and Imputation
When multiple markers/SNPs are genotyped in a gene or gene region, the SNPs may be in linkage disequilibrium (LD). Each individual test of association with a marker is correlated with all tests for other markers in LD with that marker.
So, instead of testing the individual markers for association, we may want to test haplotypes of markers for association.
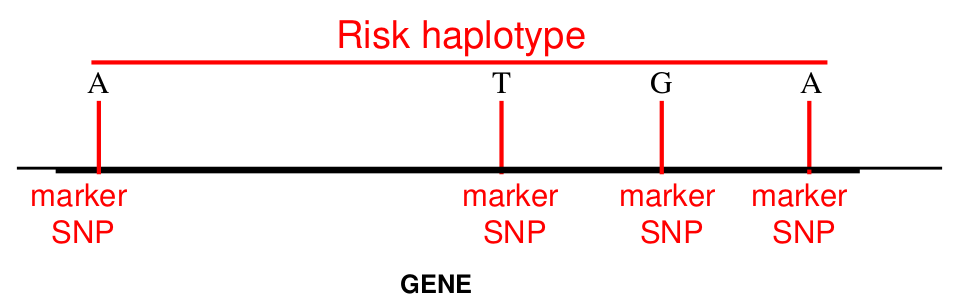
Review: A haplotype is a combination of alleles at multiple loci that are transmitted together on the same chromosome. It should provide the alleles present on the locus and which alleles are on the same chromosome. For example, if we have 2 SNPs with alleles (A, a) and (B, b) then we have 2x2= 4 possible haplotypes: AB, Ab, aB, ab.
For linked SNPs within a gene or small chromosomal region there are typically far fewer haplotypes observed than are theoretically possible (as a consquence of LD).
Reasons to Care About Haplotypes
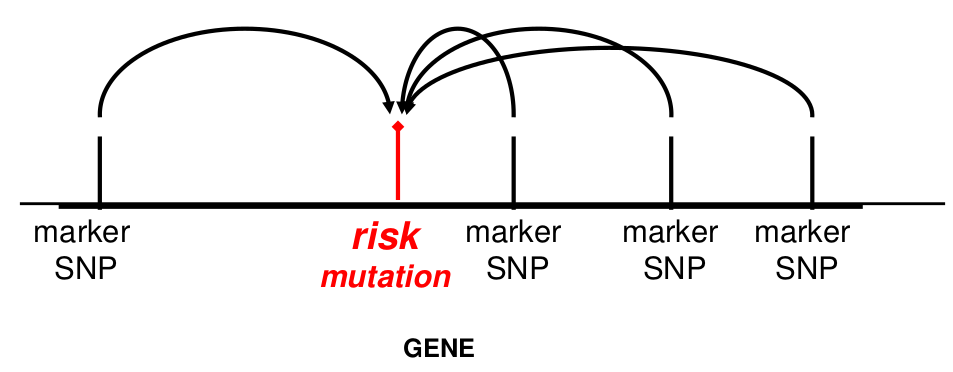
- We haven't typed the casual variant. The haplotype that the variant lies on is a better surrogate for the variant than any one SNP in the haplotype.
- The "causal" genetic variant is actually the haplotype, not any one variant -- The haplotype confers risk rather than an individual SNP allele.
- They allow us to impute additional ungenotyped variants
Often we don't have family data to help us. Haplotype phase is ambiguous only if there are 2 or more heterozygous genotypes. For example, Aa Bb genotype has two possible phases: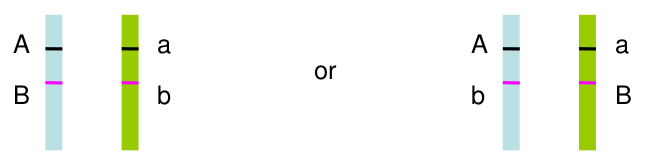
All multi-locus genotypes that consist of 2 or more heterozygotes have ambiguous phase.
When family data is not available to determine haplotypes, multi-locus haplotype probabilities and frequencies can be estimated.
Haplotype Inference
The goal is to get the probability of a haplotype given the individual's genotype. There are two classes of algorithms: EM or MCMC
- EM requires HWE assumption; MCMC does not
- EM algorithm is memory demanding to infer haplotypes for a large number of SNPs; MCMC method requires much less memory but more time
There are many options for software for phasing with and without family data.
The basic idea is to determine haplotype frequencies for sets of SNPs in close proximity on a chromosome, and compare frequencies in cases and controls or by quantitative phenotype.
Which SNPs should we use to test with Haplotypes?
- Options include:
- All SNPs on a chromosome
- All SNPs on a "haplotype block" (chromosome segment where all variants are in high LD)
- Sliding windows of 2-5 SNPs across region of interest
- Unless there is high LD, there will be more haplotypes than SNPs -> create haplotypes from SNPs that are in LD
Regression with Haplotypes/Likelihood-Based Tests
Take the following example with 3 SNPs and 4 observed Haplotypes, where each person i has 2 haplotypes: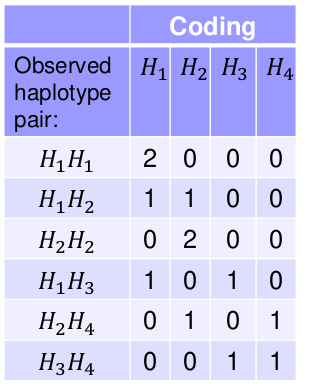
We can use variables to count the number of each haplotype type per person. This coding works for any type of multi-allelic marker, not just haplotypes.
We can use a linear regression model with the haplotype counts as predictors: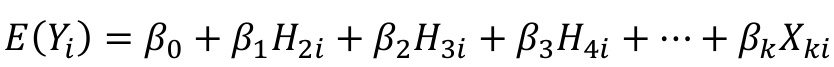
Note we do not include H1 in the model. Since H1 + H2 + H3 + H4 = 2, we already know H1 once we know the remaining haplotypes. Think of H1 as a reference haplotype.
Each individual will have a 0, 1, or 2 for each of the 3 indicator variables for the haplotypes.
For 4 haplotypes, the general (Omnibus) test for association would be:
H0: Beta1 = Beta2 = Beta3 = 0; df = 3
If we reject the null, the do tests on individual haplotypes
Global (omnibus) tests of haplotype association provide some protection from the multiple testing problem, as it tests whether the haplotype distribution is associated with phenotype.
In reality we rarely know haplotypes with certainty. Instead, for each individual haplotype estimation produces the probability of each possible haplotype pair. Can use the same model, but replace the observed haplotype counts with the expected counts (determined by probabilities).
SNP Imputation
The most recent application of haplotypes is imputation. The idea is we use a reference population that has denser genotyping of whole genome sequencing on your subset of SNPs plus many additional SNPs to impute the SNPs not typed on your chip.
A reference population is a set of individuals who have been genotyped or sequenced in a comprehensive manner. Typically these are for the whole genome sequenced (all the SNPs are included in the sample, plus many additional).
The HapMap project was the first available reference population. HRC created a large reference panel of human haplotypes by combining together sequencing data from multiple cohorts (current release consists of 64,976 haplotypes at ~39 million SNPs). TOPmed has a set of haplotypes from 97,256 genome sequenced individuals, more diverse than HRC.
The two commonly used methods for imputation are IMPUTE and Minimac, and some organizations have "imputation servers" so you can impute your GWAS data to large sequenced data sets without needing powerful on-site computers.
"Dosage"
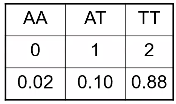
Genotype imputation does not assign a genotype to each individual, instead for each individual it assigns a probability for each of the possible genotypes at each genetic variant.
Analysis is then performed on the "dosage" - the expected genotype. The most common model is additive, but one could also use a dominant or recessive dosage.
"Best Guess Genotype"
Another method is "best guess" genotype. This is the genotype with highest probability. It ignores uncertainty in genotype assignment. We usually impose a posterior probability threshold; If p < Q, genotype is set to missing (typically set to .8, .9 or .95)
Imputation Accuracy
The overall quality of imputed data depends on how well matched the reference samples are to the samples you are trying to impute.
The concordance of imputed genotypes with true (unknown) genotypes also depends on how much information about the ungenotyped SNPs (how strong is the LD between ungenotyped and genotyped SNPs?)
For high information the concordance reaches nearly 100%, for low information regions it can be much lower.
Imputation R2 is an estimate of the squared correlation between imputed and true genotypes. It can be estimated by the obs/exp variance ratio: ratio of empirical genotype dose variance to expected (binomial) genotype variant.
Due to excess homozygosity in a well imputed variant, R2 will occasionally be more than 1.
This imputation quality measure is also a measure of the correlation between the imputed genotypes and true gentoypes.
Typically:
- R2 >= .8 is good imputation
- R2 < .3 is bad imputation
- .3 >= R2 < .8 is moderate quality imputation can be used in analysis
Good imputation:
- Has a imputed genotype dosage close to the individuals true (unknown) genotype
- Allele frequency estimated from the imputed genotypes is close to the true frequency
- Under HWE, genotypes should have frequency q2, 2pq, p2 and genotype variance 2pq (binomial distribution)
- The best possible imputation will have a sample variance of G_hat which is the same as the binomial variance, and R2 = 1
The worst possible imputation is when we have no information about the genotypes other than the allele frequency (which can be estimated from the reference haplotypes). In this case, the imputation would assign everyone the genotype probabilities q2, 2pq, p2. Thus everyone would have the same genotype dosage: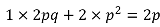
Variance would be 0 because there is no LD between SNPs, and thus correlation would be 0.
Why Impute Genotypes?
- Fill in missing genotype data
- Can test ungenotyped SNPs (with some error) for association
- Analysis of individual SNPs are easier to interpret than haplotypes
- Simplifies combining results from genome-wide association studies using different genotyping platforms
We can also combine studies to increase sample size, and thus the power. The problem is when studies use different reference SNPs, which is why the common SNPs across platforms is small. There are 2 ways to combine studies:
- Combined (joint or pooled)
- Combine individual data from multiple cohorts
- Often not feasible because of patient confidentiality
- Meta analysis
- Combining evidence for assocation across studies
- Can combine test statistics, p-value or effect size estimates (i.e. regression parameters)


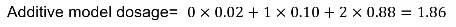
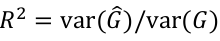
No Comments