Module 8: Interval Estimation
- θ is fixed while θhat_n is a random variable which provides the single best value to estimate θ
- θhat is unbiased when bias = E(θhat_n) - θ = 0
- θhat is consistent when θhat_n -> θ
- Mean squared error MSE = E(θhat_n - θ)2 = bias(θhat_n) + V(θhat_n)
- If bias -> and se -> as n -> infinity then θhat_n is consistent
- Probability is stronger than samples, probability standard error eventually converges to 0 as n approaches infinity but samples converge to a normal distribution which is not necessarily the same as the population distribution.
- We the estimator variability (se) to provide an interval of parameter values that are "supported" by the sample.
A 1 - α confidence interval for a parameter θ is an interval Cn = (a; b) where a = a(X1, ...Xn) and b = b(X1, ...Xn) are functions of the data such that: P(θ ∈ Cn) >= 1 - α ; Where θ is the actual population mean. Cn is random and θ is fixed.
The confidence interval (a; b) capture the true mean with confidence 1 - α. We commonly use 95% confidence intervals which corresponds to α = .05. This does NOT mean there is 1- α chance/probability the parameter falls in the interval. The correct interpretation: If we repeatedly take samples of size n from a fixed and stable population and build a 95% confidence intervals, 95% of these intervals would contain the true unknown parameter.
CI For Mean of a Normal Distribution
If σ2 is known: Xbar +/- Zα/2*αx
If σ2 is unknown: Xbar +/- t(α/2,n-1)*S/sqrt(n); Where S2 = 1/(n-1) * sum(xi-xbar)2
Using S in place of SD causes more uncertainty, thus increasing the size of the CI.
We can similarly find the confidence interval of a proportion in a similar manner:
Chi-Square DIstribution
The above represents the chi-squared distribution with n degrees of freedom. E(Q) = n and V(Q) = 2n.
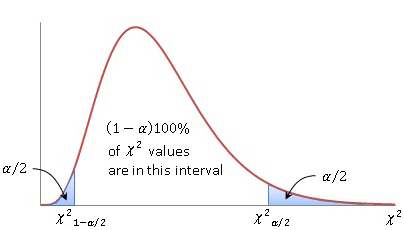
The distribution of X2n-1 is not symmetrical, so instead of centering our CI (a,b) on the mean, we look for symmetry so that the bounds P(θ < a) = α/2 and P(θ > b) = α/2.
We derive the variance of a distribution through Fisher's theorem (not shown). The CI comes out to:
Pearson's product Moment Correlation Coefficient is between -1 and 1 and represents the correlation between 2 variables.
Although rarely used, you could find a confidence interval for this value.

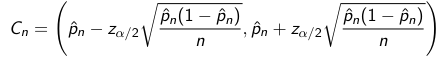
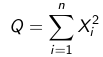
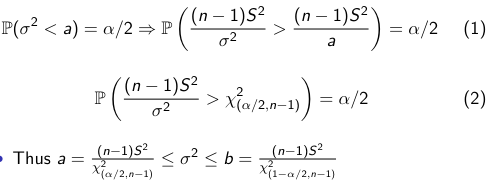
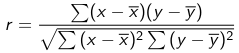
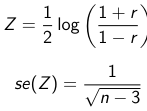
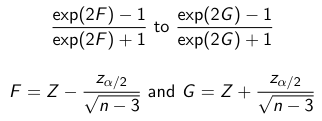
No Comments