Module 2: Probability
Probability is the study of uncertainty and randomness in the world. It measures chance.
Proportion is a summary statistic. Proportion measures size (i.e. how many patients have optional blood pressure).
- We show the probability of Event A as P(A)
- The compliment of an event, or chance of event not occurring is AC
- P(A) + P(AC) = 1
- Two events are mutually exclusive (or "disjoint") if when one event occurs the other cannot
- Two events are independent if the probability of one has no impact on the occurrence of the other
- Events are independent if:
- P(A|B) = P(A)
- P(A|B) = P(A| not B)
- Odds ratio = 1 (binary outcome)
- Events are independent if:
- If two events are not independent they are said to be statistically associated
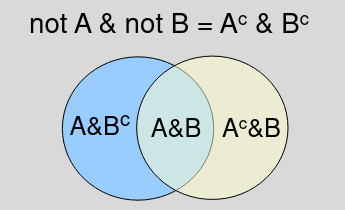
- Joint Probability = P(A & B) = P(A,B) = P(A ꓵ B)
- If A and B are independent events: P(A & B) = P(A) * P(B)
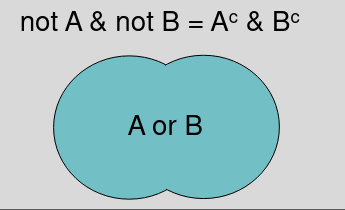
- P(A or B) = P(A U B)
- When A and B are non-mutually exclusive P(A or B) = P(A) + P(B) - P(A & B)
- When A and B are mutually exclusive events P(A or B) = P(A) + P(B) since P(A&B)=0
- Conditional probability is the chance of an event occurring given that another event occurred, written as P(A|B) = The probability of A given B.
- P(A|B) = P(A&B)/P(B)
- P(A|B) * P(B) = P(A & B)
Bayes' Theorem
Because P(A & B) = P(B & A),
P(A & B) = P(B & A) = P(B|A) × P(A)
=
P(A|B) × P(B) = P(B|A) × P(A)
P(B|A) = P(A|B) * P(B) / P(A)
Sensitivity
Sensitivity of a screening test = Probability of positive test given the person has the disease. If X is the test result and Y represents if the person actually has the disease, this can be expressed as P(X = +| Y = +) = the probability of a disease given the test was positive.
Sensitivity = True Positive Fraction = P(Test+ | Disease)
Specificity = True Negative Fraction = P(Test - | No Disease)
False Positive = P(Test + | No Disease)
False negative = P(Test - | Disease)
Positive Predictive Value = P(Disease | Test +)
Negative Predictive Value = P(No Disease | Test -)
Odds Ratio
Odds ratio can be used to check independence, events are independent when OR=1.
OR = ( P(X = +| Y = +) / P(X = -| Y = +) ) / ( P(X = +| Y = -) / P(X = -| Y = -) )
= ( P(X = +| Y = +) * P(X = -| Y = -) ) / ( P(X = +| Y = -) * P(X = -| Y = +) )
Symmetry of Odds Ratio

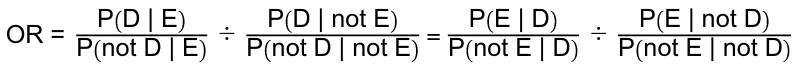
No Comments