Skip to main content

Module 14: Topics in Linear Regression

Assumption in Linear Regression:

  • Independence between observations
  • Linearity between X and Y
  • Homoscedasticity - the variance of Y is the same for any value of X
  • Normally distributed Y for any fixed value of X

Also, the model is also only generalizable to the population within the range of observed values of X.

Independence

The way we collect data or which data we collect determines independence. Examples of violated independence:

  • Data comes from individuals that are related closely
  • Multiple observations were collected over time for the same subject

Linearity

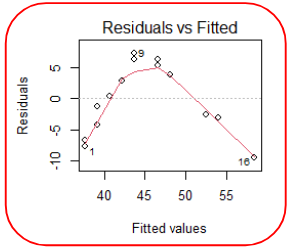
In order to test linearity, we would expect a graph of the residuals to be randomly scattered around the horizontal line. If there is a pattern to the residuals, the trend cannot be assumed to be linear.

image-1662042808164.png

The above residual plot shows a clear trend, thus the linear assumption is voilated.

Homoscedasticity

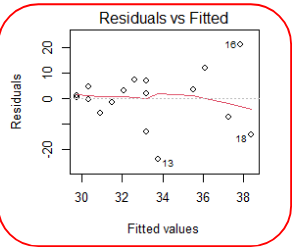
When talking about homoscedasticity, we require variance of error terms to be similar across independent variables. To assess homoscedasticity we can look at a scatterplot of y vs. x to determine if the spread in y is the same for each value of x.

image-1662042757081.png

Here we observe the spread of Y increasing as X increasing, thus the homoscedasticity assumption is not met.

Normality

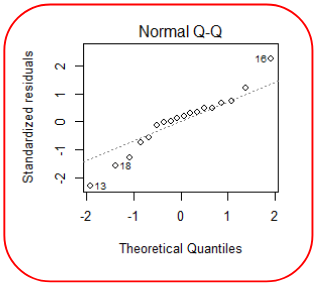
Finally for the normality of data we can examining the histogram of residuals and the QQ plot of residuals. If the data is normally distributed, the points will lie on the line.

image-1662043103274.png

Above is a example were the QQ of the residuals indicates a violation of normality.

Problem Points

Problem points can be categorized as outliers, leverage points, or influential points. A point can be any or all 3.

  • Outliers are defines one or more observations that has a large residual. In other words the observed value for the point is much different that that predicted by the model.
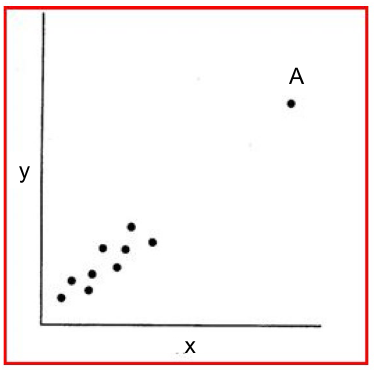
  • Leverage Points are observations which have a value of x that is far away from the mean of x.
  • Influential Observations is an observation that changes the slope of the line. One method to find these points is comparing the fit of the model with and without each observation.

image-1662043871300.png

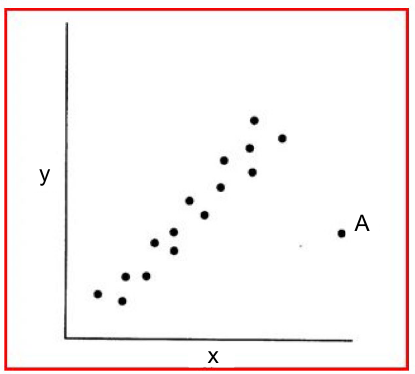
The point A above is a leverage point, but not an outlier or an influential observation.

image-1662043940655.png

Here point A is an outlier and an influential observation, but not really a leverage point.

What if the assumptions are not met?

  • If linearity is not met, you should consider other models (e.g. quadratic or logistic)
  • If normality is not met:
    • For correlation analysis we can use Spearman correlation instead of Pearson correlation
    • For regression analysis, we can investigate transformations such as log or square root
Spearman Correlation

For use when data is not normally distributed. Sort the data from smallest to largest and create ranks for both X and Y, then calculate the usual correlation on the ranked values.

No Comments
Back to top