Logistic Regression in Matched Studies

In case-control studies matching cases and controls on a potential confounder improves the efficiency of a study and removes/reduces bias.

Logistic regression controlling for a stratification variable allows us to examine multiple risk factors and control for confounders that where not matched, which is advantageous over the Mantel-Haenszel for stratified analysis.

Conditional Logistic Regression

Treats the strata effect as 'nuisance parameters'; controls for the strata but does not estimate effects. Uses 'conditional likelihood' to fit the model. Estimates effects of other parameters within strata by pooling across strata.

We can analyze the data in two ways: Matched pairs or as matched sets. Where matched pairs are always cases matched with 1 control, in matched sets the case can be matched with up to four controls. Matching conditionally on pairs in called conditional analysis.

Unconditional Model (Wrong Way)

Consider a logistic function with many strata: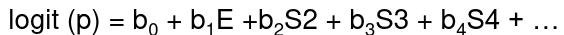
These stratum effects are nuisance parameters which contribute to the baseline risk in each stratum: b₀ + bi

The MLE maximizes this function: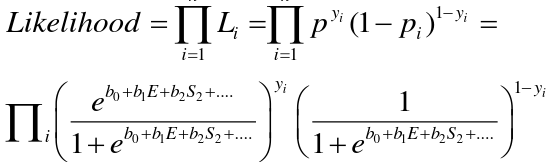
It can be shown the the odds ratio based on the MLE of b_1.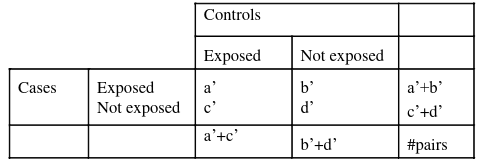

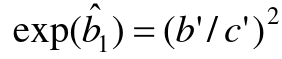
So running the above without matching gives use the wrong results. Thus, this analysis is NOT APPROPRIATE with matched pair data. We never use unconditional logistic regression for matched pairs or sets.

Correct Approach

Uses conditional likelihood approach to focus only on parameters of interest. Nuisance parameters are "conditioned" out of the analysis; no nuisance parameters in the likelihood.

Only informative strata contribute to the likelihood: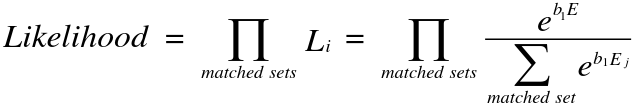
Maximum Likelihood Estimation uses likelihood on matched sets instead of individuals. We adjust for variables not matched within the matched set, or variables that cannot be practically adjusted for in regression.

Matching introduces some dependencies between subjects that cannot be ignored across strata.

Also note the Breslow-Day test has no meaning in matched sets analysis.

R Code

library(survival)

### Create variables
match <- c()
for(i in 1:63){ match <- c(match, rep(i,2))}
disease <- rep( c(1,0), 63)                          ## each pair has exposed/unexposed
exposed <- c(rep(c(1,1), 27),                        ## 27 pairs (D, E), (not D, E)
                        rep(c(1,0),                  ## 29 pairs (D, E), (not D, not E)
                        rep(c(0,1), 3),              ## 3 pairs (D, not E), (not D, E)
                        rep(c(0,0), 4))              ## 4 pairs (D, not E), (not D, not E)


### Unconditional Model - INCORRECT
mod <- glm(disease ~ exposed + factor(match), family = binomial)
summary(mod)

### Conditional Logistic Regression - CORRECT
mod <- clogit(disease ~ exposed + strata(match))
summary(mod)


### Estrodat data
## Read the data ##
estrodat <- read.csv("estrodat.csv", header=T, na.strings=".")
estrodat2 <- subset(estrodat, is.na(age)==F & is.na(gall)==F & is.na(hyper)==F 
                    & is.na(obesity)==F)
m.uni <- clogit(case ~ estro + strata(match), data = estrodat2)
summary(m.uni)

m.multi <- clogit(case ~ estro + age + gall + hyper + obesity + strata(match), data = estrodat2)
summary(m.multi)

### Uninformative sets
uninform.index <- c()
for (i in 1:length(unique(estrodat2$match))) {
  if (length(unique(estrodat2$case[ which(estrodat2$match==i)])) < 2) {
    uninform.index <- c(uninform.index, i)
  }
}
estrodat2[ which(estrodat2$match %in% uninform.index),]

estrodat3 <- estrodat2[ -which(estrodat2$match %in% uninform.index),]
### Crude Analysis
m.uni2 <- clogit(case ~ estro + strata(match), data = estrodat3)
summary(m.uni2)

m.multi2 <- clogit(case ~ estro + age + gall + hyper + obesity + strata(match),
data = estrodat3)
summary(m.multi2)