Three-Way Contingency Tables
In studying the association between two variables we should control for variables that may influence the relationship. To do so we can create K strata to control for a third variable.
When all involved variables are categorical, we can display the distribution of (E, D) as a contingency table at different levels of C.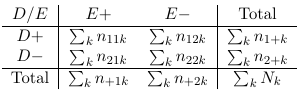
The cross-section of tables are called partial tables. The 2-way table that displays the distribution of (E,D) disregarding C is called the E-D marginal table.
Partial tables can exhibit different association than the marginal tables (Simpson's Paradox); for this reason analyzing marginal tables can be misleading.
Simpson's Paradox occurs when an association between two variables is reversed upon observing a third variable.
Independence
In 1959, Mantel and Haenszel proposed a test for independence (between E and D) while adjusting for a third variable (C). This test statistic is called the Cochran-Mantel-Haenszel test statistic and is defined as:
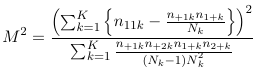
1. Under the conditional independence assumption (across all strata) M2 follows a chi-squared distribution with 1 degree of freedom.
2. M2 has good power against the alternative hypothesis of consistent patterns of association across strata.
If conditional independence assumption fails one might be interested in testing the assumption that OR is the same across the K tables. This could be done with the Breslow-Day Test for Homogeneity of Odds Ratios (reported by PROC FREQ in SAS).
title1 " Care and Infant survival in 2 clinics " ;
data care ;
input clinic survival $ count care ;
cards ;
1 died 3 0
1 died 4 1
1 lived 176 0
1 lived 293 1
2 died 17 0
2 died 2 1
2 lived 196 0
2 lived 23 1
run ;
proc freq data = care ;
table clinic * survival * care / cmh chisq relrisk ;
weight count ; run ;Note that:
- The methods outlined here apply not only to situations where the classification variables are both responses (this will be explored in a later section)
- We will cover a way to test conditional independence based on Log-Linear models next
Log-Linear Models for S x R x K Tables
Every association between three variables can be coded with a different Log-Linear model. We will select among the association patters, using the deviance GoF statistic.
Saturated Model
The number of parameters: 1 + S + R + K + RK + SK + RSK
To reduce the number of parameters we impose linear constraints on the parameters. Consider the following examples:
Reference Coding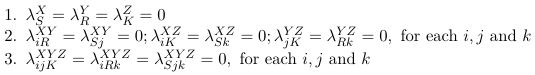
Effect Coding (Zero Sum Constraints)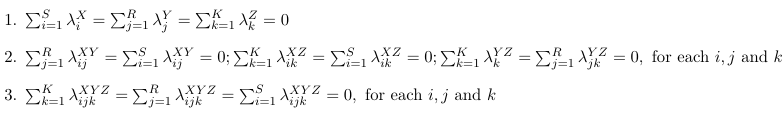
In the saturated model the number of parameters is:
1+(S - 1)+(R - 1)+(K −1)+(S −1)(R−1)+(S −1)(K −1)+(R−1)(K −1)+(S −1)(R−1)(K −1) = SRK
Note that with the saturated model we make no assumption regarding the association among variables.
All Two-Way Interaction Model
Let's consider another model with all two-way interactions (no three-factor interaction):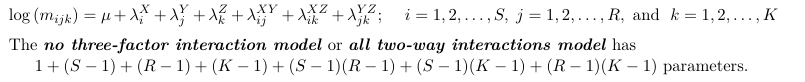
Under this model the association between X and Y is the same between different levels of Z; The association between X and Z is the same at different levels of Y; and the association between Z and Y is the same at different levels of X.
We can actually do the math and o serve that the Odds Ratio between X and Y (ORKXY) is the same at all levels of Z (it does not depend on k):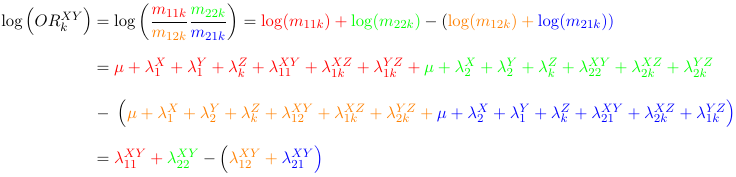
Mutual Independence Model
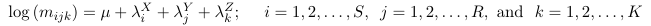
No interactions, the model assumes X, Y and Z are mutually independent.
The number of parameters will be: 1 + (S - 1) + (R - 1) + (K - 1)
Again, here the partial and marginal odds ratio between X and Y is 1 and does not depend on the level of Z.
Conditional Independence Models
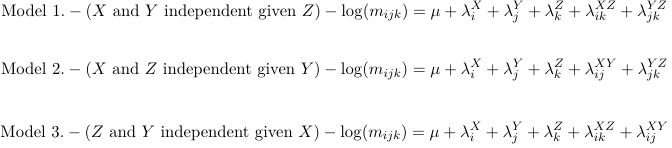
Model 1 will have number of parameters: 1 + (S − 1) + (R − 1) + (K − 1) + (S − 1)(K − 1) + (R − 1)(K − 1)
Joint Independence Models
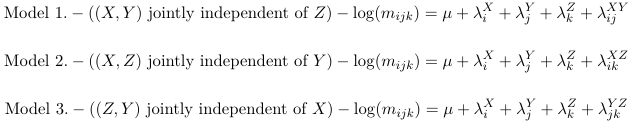
With the first having number of parameters: 1 + (S − 1) + (R − 1) + (K − 1) + (S − 1)(R − 1)
Graphs
Each of these models is hierarchical and can be represented by a association graph. This is a graph which represents which variables are independent, conditionally independent or associated.
The number of vertices is equal to number of variables, and edges represent partial association between he corresponding variables.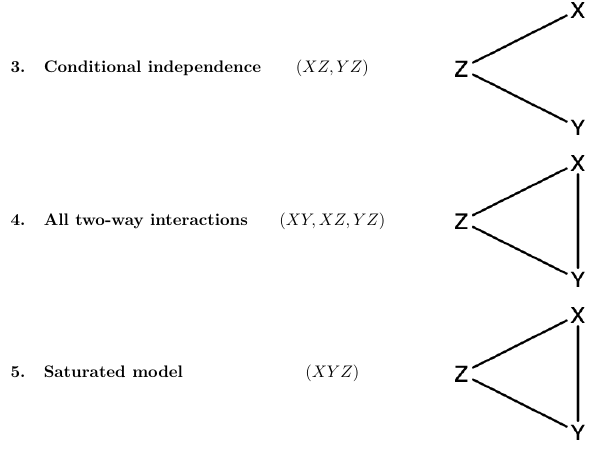
Modeling Strategy
- Model Selection
- The likelihood ratio statistics can be broken down conditionally; Given two nested models the G2(M2 | M1) = G2(M2) - G2(M1), measures the additional contribution to the fit of the model M1 over M2 and (under the assumption M2 holds) will follow a chi-square distribution with p1 - p2 df
- Use all your subject matter knowledge searching for the best model
- The number of models that should be considered increases exponentially with number of parameters
- One strategy is to first compare independence (interaction and saturation model); Then identify the simplest model in between this model and the nested model.
- The test statistics are independent and one should adjust the significance level for multiple testing.
- The likelihood ratio statistics can be broken down conditionally; Given two nested models the G2(M2 | M1) = G2(M2) - G2(M1), measures the additional contribution to the fit of the model M1 over M2 and (under the assumption M2 holds) will follow a chi-square distribution with p1 - p2 df
- Occam's razor pinciple (All things being equal, the simplest solution tends to be the best one) - If the difference in Likelihood ratios is not significant, choose the more parsimonious model
- Structural zero cells are cells for which it is impossible to have a count greater than 0; These should be treated differently than 0s that happen by design (Sampling Zeros). One practice is to add a small constant (.0001).
Higher Dimension tables
Three way tables are significantly more complicated than two-way tables due to the fact that the number of interaction terms increases and the possible association among variables increases. With higher dimension tables, the number of cells increase exponentially. This creates problems with inferences as we require a larger data set in which some cases might not be available. If the data does exist though, then we can use the same strategy for model fit and selection.
SAS Code
data THR ;
input Rural Income Satisf Count ;
datalines ;
1 1 1 48
1 1 2 12
1 2 1 96
1 2 2 94
2 1 1 55
16
BS853 - Generalized Linear Models
Spring 2023
2 1 2 135
2 2 1 7
2 2 2 53
run ;
title1 ’ Association among residence , income and satisf with total hip replacement ( THR ) ’;
options ps =60 ls =89 pageno =1 nodate ;
title2 ’ Model 1 saturated model ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural | Income | Satisf / dist = poissonrun ;
obstats type3 ;
title2 ’ Model 2 - all two - way interactions ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural | Income Rural | Satisf Satisf | Income / dist = poisson obstats type3 ;
run ;
title2 ’ Model 3 - conditional independence of Income and Rural ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural | Satisf Satisf | Income / dist = poisson obstats type3 ;
run ;
title2 ’ Model 4 - conditional independence of Satisfaction and Rural ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural | Income Satisf | Income / dist = poisson obstats type3 ;
run ;
title2 ’ Model 5 - conditional independence of Satisfaction and Income ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural | Income Rural | Satisf / dist = poisson obstats type3 ;
run ;
title2 ’ Model 6 - joint independence of ( Income and Satisfaction ) from Rural ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural Satisf | Income / dist = poisson obstats type3 ;
run ;
title2 ’ Model 7 - joint independence of ( Income and Rural ) from Satisfaction ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural | Income Satisf / dist = poisson obstats type3 ;
run ;
title2 ’ Model 8 - joint independence of ( Rural and Satisfaction ) from Income ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural | Satisf Income / dist = poisson obstats type3 ;
run ;
title2 ’ Model 9 - Mutual independence of Income , Rural , and Satisfaction ’;
ods select ModelFit ;
proc genmod data = THR ;
class Rural Income Satisf ;
model count = Rural Satisf Income / dist = poisson obstats type3 ;
run ;
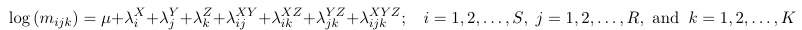
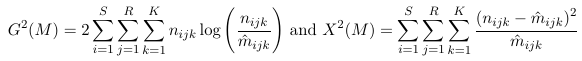
No Comments