Non-Inferiority in Clinical Trials
Usually clinical trials should show if a new treatment is superior to placebo or no treatment, but as we've previously discussed it is not always ethical to give out a placebo when an effective treatment has been identified.
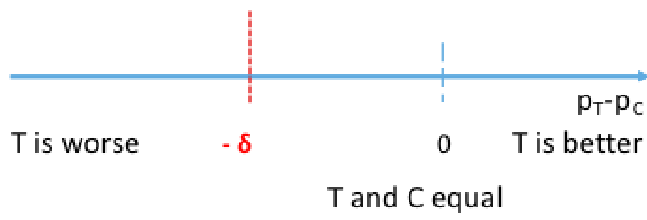
The goal of non-inferiority trials is to to demonstrate a new treatment (T) is NOT inferior (no worse than) the best available treatment (C), given the effect of the active control (compared to placebo or no treatment) has already been established.
Non-Inferior = Not Unacceptably Worse
In practice non-inferiority trials assess:
- If T is not necessarily more efficacious (superior) than C
- If T could be not as effective as C, but could have potential ancillary benefits:
- Lower procedural risks (safety)
- Less side effects
- Improved convenience
- Favorable costs
- Non-inferiority margin: How much worse we are willing to accept T compared with C
Hypothesis Testing
H0: πT - πC <= -δ (inferior)
HA: πT - πC > -δ (non-inferior)
π represents the population level experimental and control proportions/risk of outcome
δ is the non-inferiority margin
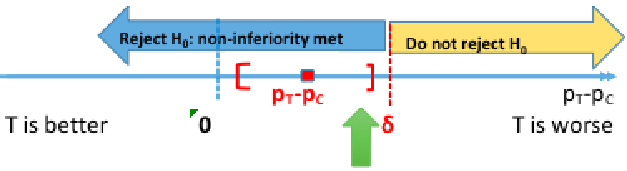
Rejecting the null means non-inferiority is met, failing to reject the null means the new treatment is inferior. Both non-inferiority and superiority are met if T falls above the 'T and C' are equal point.
The null can also be rewritten as πT + δ <= πC, but SAS uses: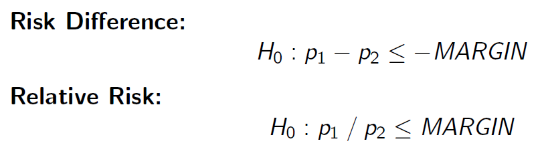
Because these settings cannot be changed, consider your margin carefully
Computing the 95% confidence interval for the difference in πT - πC we would reject the null when the CI's lower boundary is greater than -δ.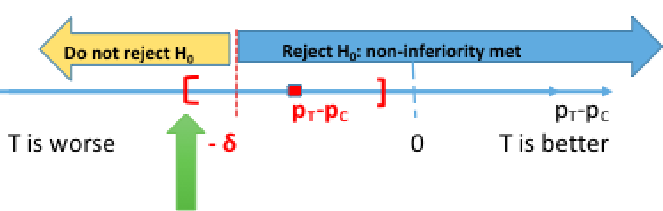
This is because we are only computing a one-sided test. Note that SAS gives us both sides of the confidence interval, so it is important to know which side is being tested.
Binary Outcomes - Farrington-Manning Test
Below is a Z test statistic following a normal approximation to the binomial distribution: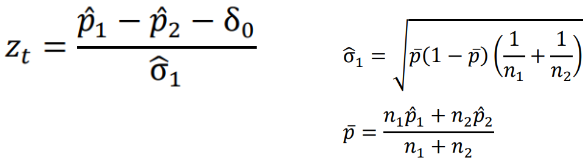
The Farrington-Manning Test (used in SAS) uses restricted maximum likelihood estimation to estimate variance of risk difference or risk ratio under non-inferiority null: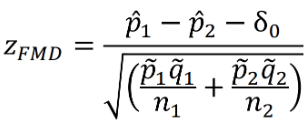
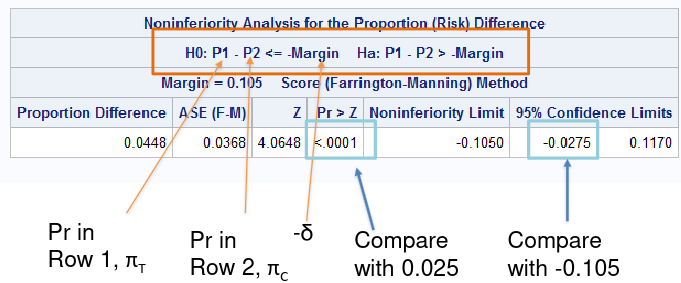
Also note the the FDA requirement for non-inferiority is alpha=.025.
In the SAS sample code below we test the positive outcome of HVC treatment, testing a margin of .105:
data hepatitis;
input trt outcome count;
cards;
24 0 13
24 1 149
48 0 20
48 1 140
;
run;
*Positive Outcome;
proc freq data=hepatitis;
table trt*outcome/riskdiff(column=2 noninf method=fm margin=0.105) alpha=0.025;
weight count;
run;In a negative outcome, where we are testing if something is made worse, we would look at the upper boundary of the confidence interval compared to -δ.
So far we've been testing the risk difference, but we may want to test the relative risk (AKA risk ratio) of outcome. Then our null hypothesis would look like: H0: πT / πC >= R
Keep in mind when considering risk ratio or risk difference:
For a negative outcome:
- It takes a larger sample to prove non-inferiority using the RR approach than absolute RD approach
- A sample size yielding power of 80% with risk difference only yields about 70% power with RR approach
For a positive outcome:
- It takes a larger sample to prove non-inferiority using the RD approach than RR
*Sample Size - Risk Difference;
proc power;
twosamplefreq alpha=0.025
groupproportions = (0.30, 0.30)
test=fm
sides=1
power=0.80
nullproportiondiff = 0.10 0.20
npergroup=.;
run;
*Sample Size - Risk Ratio;
proc power;
twosamplefreq alpha=0.025
groupproportions = (0.30, 0.30)
test=fm_rr
sides=1
power=0.80
nullrelativerisk = 1.67 1.33
npergroup=.
;
run;Choice of Inferiority Margin
The trial should have the ability to recognize when the new drug T is not inferior to the active control C and superior to the placebo P by a specified amount.
The two-step procedure proposed by the FDA Guidance on Non-Inferiority trials (updated 2016), for a risk difference approach:
- Define M1: Effect of active control relative to placebo (πT - πC or its best estimate)
- M1 is the smallest (most conservative) estimate of C against P
- M1 must be > 0, otherwise there is no evidence that C is superior to P
- Average/combine placebo minus control RD from previous placebo vs the control trial (e.g. via meta-analysis)
- Define M2: The non-inferiority margin is HALF of M1
- M2 is the largest clinically acceptable difference (degree of inferiority) of the test drug compared to the active control
- Should be set as <= .5*M1
Issues in Non-Inferiority Trials
There are several challenges with non-inferiority trials for investigators and regulatory bodies:
- Assay sensitivity
- A trial that demonstrates non-inferiority does not demonstrate efficacy
- Both C and T could be similarly ineffective
- In non-inferiority trials we make an (untestable) assumption that the control treatment is effective (assay sensitivity) in the trial setting
- Factors that may induce assay insensitivity: lower event rates, poor adherence, new concomitant medications, etc. compared to the placebo-controlled trials
- A related concept is assay constancy: the treatment effect of C s no treatment P is the same as in the trials which informed the choice of margin
- A trial that demonstrates non-inferiority does not demonstrate efficacy
- Less incentives to reduce errors
- Factors that reduce the difference between treatments (measurement error, low event rates, adherence, etc) will increase the likelihood of declaring non-inferiority (success)
- Unlikely in superiority trials, bias toward the null improves the chance of trial success
- Efficacy creep
- Efficacy creep or biocreep can occur when a slightly inferior treatment becomes the new standard of care for the next gen non-inferiority trials
- If it happens repeatedly we end up with a standard of care no better than the placebo
- Degradation of the true efficacy of the comparative drug
- Ideally a control treatment C should have been previously known to be effective against placebo P directly
- Primary approach to analysis (ITT or PP)
- Intention to treat (ITT) is often considered the primary approach to analysis, but ITT is known to make groups appear more similar mostly due to including subject who are non-compliant
- Per-protocol (PP) can make groups appear more similar or more different
- If we use PP instead we lose benefits of randomization (by removing non-compliant participants)

No Comments