Skip to main content

Hierarchical Models

Previously we have assumed given covariates, the observations are independent. However, there are many situations where this does not hold. Bayesian Hierarchical models can be used to cluster observations, where each cluster might have its own cluster-specific parameters.

In Bayesian hierarchical models, we start by imposing a prior that is a function of different parameters. We'll introduce a new variable γ, which is called the hyper-prior; The prior of α depends on β, which depends on γ.
image.png
Hyper-parameters: Parameters of prior distribution
Hyper-Priors: Distribution of Hyper-parameters

A typical example of this in medical research is population of hospitals, providers within hospitals, and patients within providers. Any datasets with such a structure are called hierarchical. Hierarchical models are also called partial pooled or random effect models.

We are interested in making inference of specific units. In doing so observations may be collected over time on the same individuals, so repeated measures must be accounted for.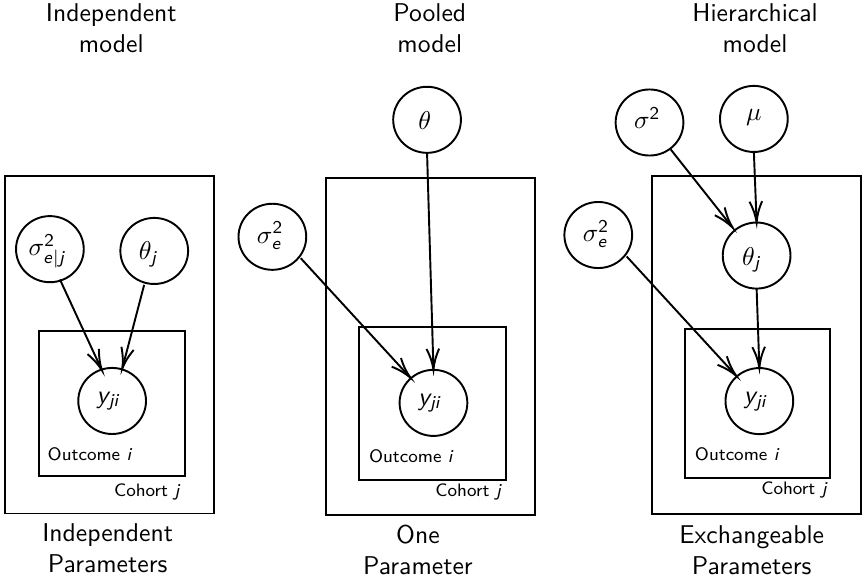
image.png

  • Independent models have no randomly-varying effects
  • Pooled models have a randomly-varying (subject-specific) effects of slope
  • Hierarchical h ave randomly-varying (subject specific) effects of slope and intercept

Ranking Posterior Estimates

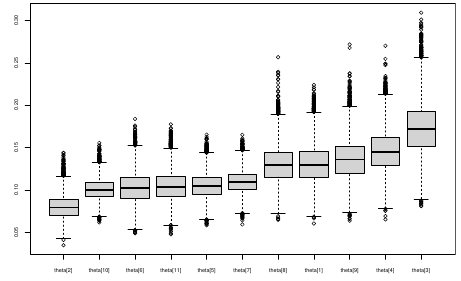
image.png
We can simply rank the outcome/results in a box plot such as the above, but this does not consider the uncertainty of the estimates.

We can derive the posterior distribution of each ranking by ranking the estimates at each iteration of the Gibbs Sampling and generate the posterior distributions of the ranks. Below the ranks are in parenthesis:
image.png
The posterior distribution of ranks gives us a measure of the uncertainty of the ordering.

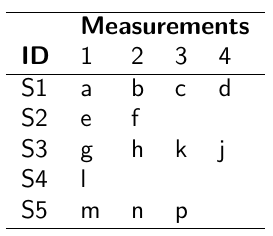
Data Formatting

There are three main alternative approaches to account for the hierarchical structure of the data in coding, in order of popularity:

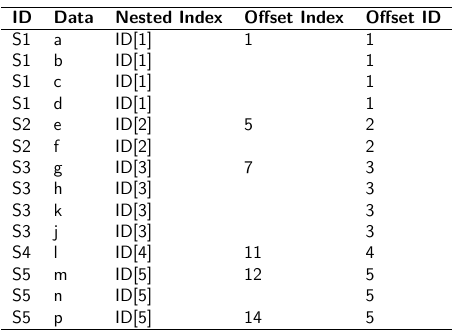
  1. Nested Indexes - Define an index of the same length of the data that specifies the cluster to which each unit belongs.
  2. Offset - Construct a vector of indexes that define the first and last element of each cluster. Needs two indexes

    Tabular Format: image.png Long Format: image.png

  3. Data padding - Structure data in array format and fill in empty cells with NA when clusters include different sample sizes
Model Implementation With Offset
### Begin by setting up the data and generating the offset
## Prepare outcome and covariate data
y <- na.omit(c(t(HB.data[, 6:8]))) # All outcome data
y0 <- HB.data[, 5] # Baseline data
t <- c(t(HB.data[, c(2, 3, 4)]))[-na.action(y)] # Times corresponding to non-missing outcome

## Fill in data for offset indexes one subject at a time, starting with the first subject
i <- 1
offset <- c(1, 1 + length(which(is.na(HB.data[1, 6:8]) == F)))

## Add a new offset for each subject until the end of data
while (offset[(i + 1)] < length(y) - 1) {
	i <- i + 1
	offset <- c(offset, offset[i] + length(which(is.na(HB.data[i,6:8]) == F))) # Calculate offsett for subject i
}
offset <- c(offset, (length(y) + 1)) # Concatenate to the set of offsets

model.1 <- "model {
	for (i in 1:N) {
		for(j in offset[i] : (offset[i+1]-1)){
			y[j] ~ dnorm(psi[j], tau.y)
			psi[j] <- alpha[i] + beta[i]*(t[j] - tbar)
				+ gamma*(y0[i] - y0bar)
		}
	alpha[i] ~ dnorm(mu.alpha, tau.alpha)
	beta[i] ~ dnorm(mu.beta, tau.beta)
	}
	# priors
	sigma.a <- 1/tau.alpha
	sigma.b <- 1/tau.beta
	sigma.y <- 1/tau.y
	mu.alpha ~ dnorm(0, 0.0001)
	mu.beta ~ dnorm(0, 0.0001)
	gamma ~ dnorm(0, 0.0001)
	tau.alpha ~dgamma(1,1)
	tau.beta ~dgamma(1,1)
	tau.y ~dgamma(1,1)
	y0bar <- mean(y0[])
	tbar <- mean(t[])
}"

i = subject
offset[i]: (offset[i + 1] -1) = observations corresponding to subject i

image.png

Checking Convergence

The major assumption of MCMC is convergence. There are 4 widely-used diagnostic plots in R:

  • Gelman and Rubin: With M >= 2 chains calculate the potential scale reduction factor as ratio of estimated variance of the parameter and within-chain variance
  • Gewke: Test for equality of means between two non-overlapping parts of the Markov Chain
  • Raftery and Lewis: Calculates the number of iterations N and the number of burn-ins M necessary for a quantile of interest q to be estimated with an acceptable tolerance r (in (q-r, q+r)) with a probability s
  • Heidelberg and Welch: Calculates a test statistic to test the null hypothesis that the Markov chain is from a stationary distribution
Gelman and Rubin Diagnostics

With m chains of length n, GR convergence diagnostic provides numeric convergence summary based on multiple chains (at least 3 chains are required)

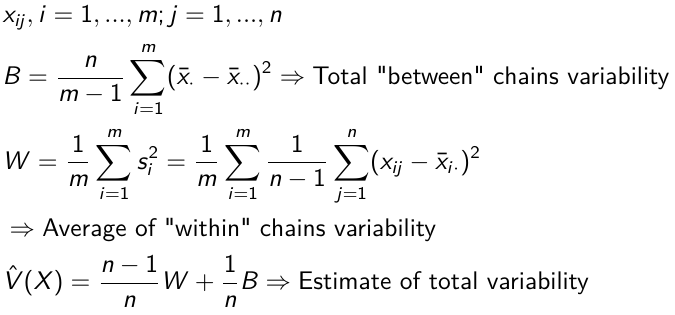
image.png
If the chains are all from stationary distributions: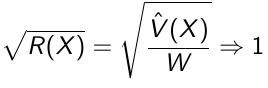
image.png

jags.snp <- jags.model(textConnection(model.snp), data = data.snp, n.adapt = 1500, n.chains = 3) 
update(jags.snp, 1000)
test.snp <- coda.samples(jags.snp, c("beta.snp"), n.iter = 1000)
geweke.diag(test.snp, frac1 = 0.1, frac2 = 0.5)
gelman.diag(test.snp)
gelman.plot(test.snp, ylim = c(1, 4))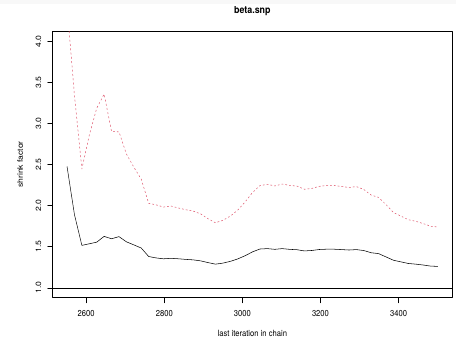

image.png
This graph is an example of chains that do not converge; They could be approaching 1 but we see a lot of variability especially near the beginning.

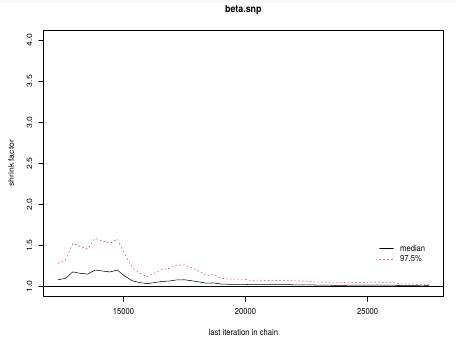
image.png
In this plot we can observe the lines converge around 1.

Note: Parallel Computing

As the number of chains for convergence increases in more complicated models we require more computing power. There are several packages in R that can be used to do this, perhaps the most used being snowfall or doParallel.

Comparing Hierarchical Models

Joint likelihood of data and parameters:
image.png

There are three primary approaches used:

  • Deviance Information Criterion (DIC)

    image.png
    Which is based on p(y | θ)

  • Akaike Information Criterion (AIC)
        AIC = -2 log(y | φ̂) + 2pφ
    where pφ is the number of hyper-parameters
  • Bayesian Information Criterion (BIC)
        BIC = -2 log(y | φ̂) + log(n)*pφ

"Likelihood" is not well defined in a hierarchical model; It depends on the "focus" of the study if we want to use θ, φ, or the model structure without any unknown parameters. It is not a matter of which is correct but which is appropriate for our purpose.

Consider an example where our model predicts classes within schools in within a country:

  • If we are interested in predicting future classes in those school then θ is the focus and deviance-based methods such as DIC are appropriate
  • If we are interested in predicting results of future schools in a country then φ is the focus and marginal-likelihood methods such as AIC are appropriate; Relevant to education within the whole country.
  • If we are interested in predicting results for a new country, then no parameters are in focus, the Bayes factors are appropriate to compare models; Relevant to general statements about education in the
  • whole world or outside of the country being studied.

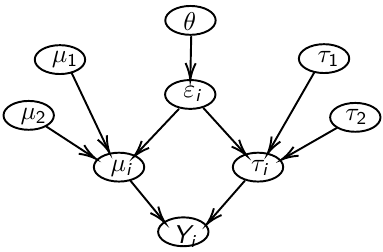
Mixture Models

Mixture models integrate multiple data generating processes into a single mode; AKA a mixture of many distributions. This is especially useful in cases where the data doesn't allow us to fully identify which observations belong to which process, such as clustering.

image.png
image.png

model.1 <- "model{
p[1] <- theta
p[2] <- 1 - theta
for( i in 1 : N ) {
	epsilon[i] ~ dcat(p[]) # dcat: categorical outcome
	y[i] ~ dnorm(mu[epsilon[i]],tau[epsilon[i]])
}
theta ~ dbeta(1,1)
for (j in 1:2){
	mu[j] ~ dnorm(0.0, .0000001);
	tau[j] ~ dgamma(1,1)
	sigma[j] <- pow(tau[j],-2)
}
}"

 ε value hidden → two profiles

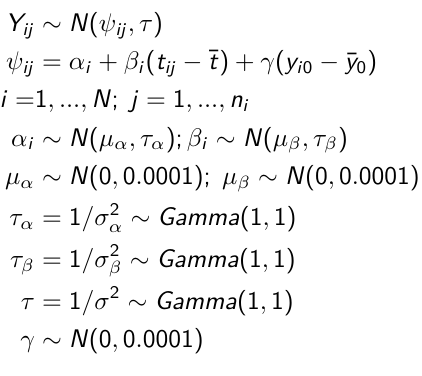
No Comments
Back to top