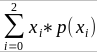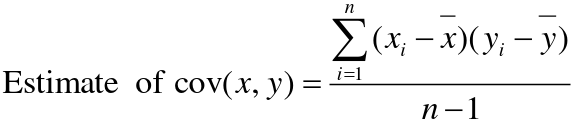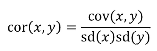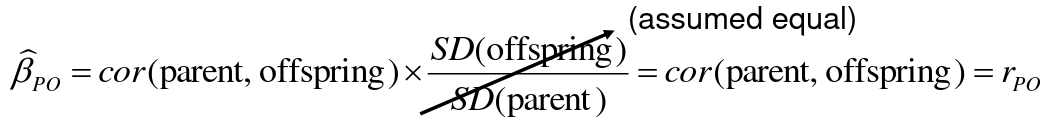Assessing the Genetic Component of a Phenotype

A phenotype is the appearance of an individual, which results from the interaction of the person's genetic makeup and their environment. Phenotypes can be categorical or numerical. If we are interested in the genetic component of a trait  there are different methods we can use for analysis.

We define a trait for analysis, determine what we are interested in studying, and then the methods that need to be used. For example, if we want to know how BMI is linked to gene effects we would need to consider other factors such as age, sex, smoking, etc. Thus, a Multiple Linear Regression might be appropriate, were we can measure the variability of each factor.

Variance of Phenotypic Traits

𝜎²_T = The observed (phenotypic) variability of a trait

𝜎²_T = 𝜎²_G + 𝜎²_E = The phenotypic variability can be partitioned in to variability due to genetic and environmental effects

𝜎²_G = 𝜎²_A + 𝜎²_D = The genetic component can be further partitioned into additive and dominance genetic variance

We can write a model for the trait as:  

T = (A + D) + E = G + E

Assumptions of this model:

• Genetic and environmental factors are uncorrelated
• Standard deviation of trait is the same for all individuals

Additive and Dominance Components

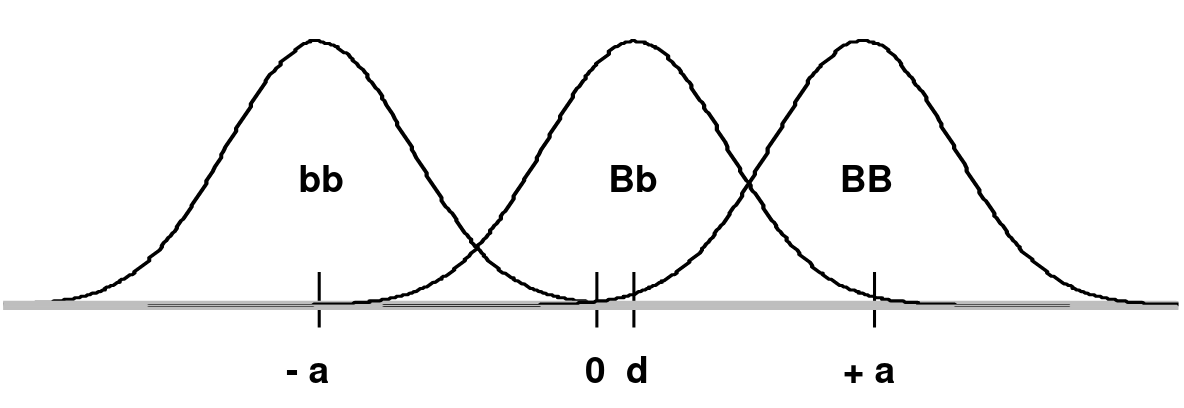
Consider a frequency distribution of trait values for two alleles B and b, where B creates a high trait value and b creates a low trait value on a continuous scale which is shifted so that the midpoint between the mean of BB (+a) and bb (-a) is 0:

d is the mean of the Bb group

In an additive model d = 0 (no dominance; dominance variance = 0)

In a recessive model: d = -a    (Bb would overlap the bb distribution)

In a dominant model d = +a   (Bb would overlap the BB distribution)

The degree of dominance can be defined as d/a

Heritability

The heritability of a trait is the proportion of total phenotypic variance that is due to genetic effects.

Heritability can be defined as:

h²    =    𝜎²_G /  𝜎²_T     =   ( 𝜎²_A + 𝜎²_D ) / ( 𝜎²_A + 𝜎²_D + 𝜎²_E )

The above formula is also called Broad sense hertiability. Narrow sense heritability (just the additive component): 

h_n²    =  𝜎²_A  / 𝜎²_T

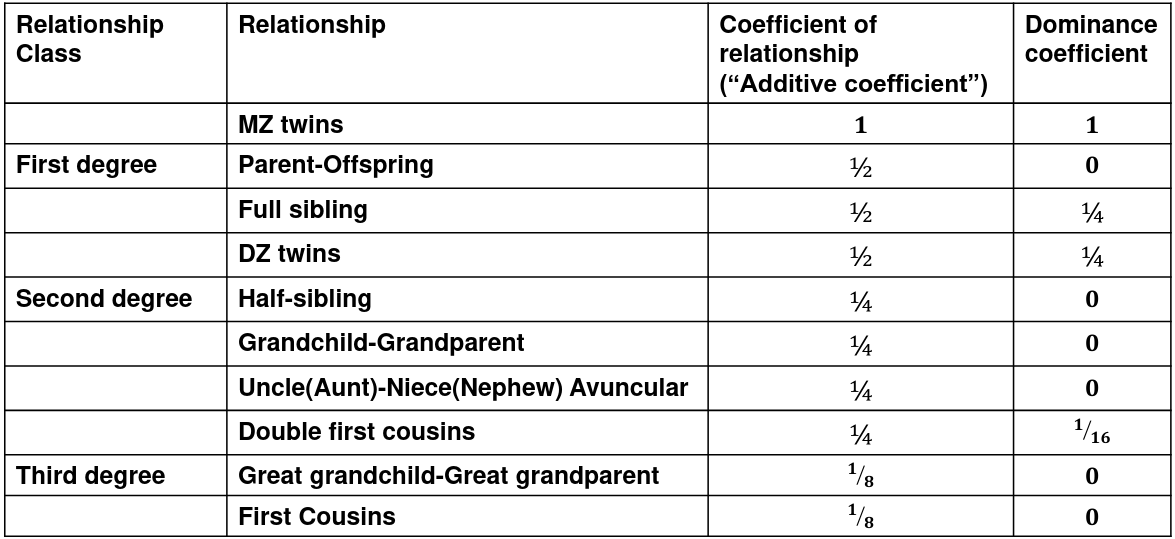
We use the expected resemblance among relatives to estimate h². It is a function of covariance between relatives and coefficient of relationship (AKA "Additive coefficent")

The additive coefficient of a relationship C is the expected proportion of alleles shared IBD by a relative pair, defined as:

C = 2^-R, where R is the degree of relationship

• R = 0: MZ twins -> C = 1
• R = 1: 1st degree relationship; sib, parent-offspring -> C = 1/2
• R = 2: 2nd degree relatives: half-sibs, grandparent-grandchild, avuncular
• R = 3: 1st cousins

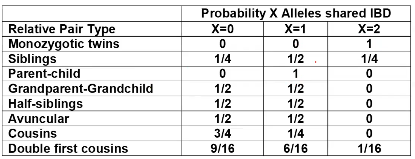
Recall sharing a allele Identical-By-Descent means relatives who share the exact same copy of an allele by inheritance.

The additive coefficient is expected proportion of alleles shared IBD by the pair, so we can also define it as

p(x) = x/2 = the proportion of shared alleles

For example, the parent child relationship would have a additive coefficient of 0*(0/2) + 1*(1/2) + 0*(2/2) = 1/2

The kinship coefficient is the probability that a randomly selected pair of alleles from a individual is IBD. It is always half of the coefficent of relationship.

Estimating Heritability

Using Co-variance

Recall the properties of covariance:

• Cov(X,Y) = Cov(Y,X)
• Cov(X, X) = var(X)
• Cov(X + Y, Z) = Cov(X, Z) + Cov(Y, Z)
• Cov(cX, Y) = c*Cov(X,  Y); where c is some constant
• The unit of covariance is xy
• Positive covariance: Value of x tends to be high when value of y is high
• Negative covariance: Value of x tends to be high when value of y is low

A standardized measure of covariance is correlation which is a scale of -1 to 1

We can use the properties of covariance to determine the covariance between quantitative measure on a parent and an offspring. This folows the same T = (A + D) + E = G + E concept as above:

Cov(Parents, Offsrping) = Cov (A_p + D_p + E_p, A_o + D_o + E_o)

In this example, we can break this down into:

• Cov (A_p, A_o) = Additive covariance, offspring always inherits exactly 1 allele from parent so = (1/2)𝜎²_A 
  
• Cov (E_p, E_o),  covariance of environmental component between parent and offspring is assumed to be 0
  
• Cov (D_p, D_o) = Since offspring do not inherit pairs of alleles the dominance environmental component is also 0
  
• The cross terms, Cov(A, D) and etc. which we assume to be 0

Note: This only works if the assumptions of independence is true and standard deviation is the same for all individuals.

Since we are assuming standard deviation is the same across generations we can write hieritability between parent and offspring as a product of correlation:

h_n² =  𝜎²_A  / 𝜎²_T = 2 * Cov(parent, offspring) / SD(parent)*SD(child) = 2 * Cor(parent, offspring)

Thus, we can estimate narrow-sense heritability using 2 times the observed correlation between parents and offspring.

Using Linear Regression

Alternatively, we can use the linear regression coefficient to estimate heritability. Where Y is offspring and X is parent:

𝑌 = 𝛼 + 𝛽𝑋 + 𝐸

 𝛽_hat ~ cor(X, Y) x SD(Y)/SD(X)

h_n² = 2*r_PO = 2*𝛽_hat_PO

Note that the estimate obtained from beta may differ from the estimate obtained from r if the standard deviations of parents and offspring are not equal.