Survival Analysis in Clinical Trials

We've already covered survival analysis in great detail here. This will be review, application to clinical trials, and SAS implementation.

Survival analysis uses class methods of studying occurrence and time of events; it was traditionally designed to study death, but can be used with any type of time to event outcome. These are special cases when a t-test is not appropriate; as the data is skewed and there are values that need to be censored before the end of study.

Participants enter the study event-free and the outcome is to assess if and when the event occurred. We can then investigate if the event occurs differently in other groups. Patients are typically randomized at different dates in the recruitment period and time is measured on a continuous scale. We measure time in the study as the time between randomization and either the patient:
    - Has the event (Failure time)
    - Is last measured in the study and does not have the event (Censoring time)

Right Censoring

Most common form of censoring and the ideal scenario; Participants are followed for a time but the event of interest does not occur. All we know is that the time of the event is greater than a certain value but it is unknown by how much.

• End of study
• Loss to follow-up (withdrawal or dis-enrollment)
• A completing risk - A different event that occurs and makes it impossible to determine when the event of interest occurs

Interval Censoring

The time for an event occurs between two time points in the study but the investigators do not know the exact date. This could occur when the outcome is self-reported at 3 month intervals, for example. There are special methods for interval censoring in SAS we will not cover here (PROC ICLIFETEST)

The Survival Function

The survival function S(t) is a mathematical function that represents the probability of surviving beyond a particular time t. We can plot the % surviving (without event) on the Y-axis and time on the X-axis to see when most of the events occurred.

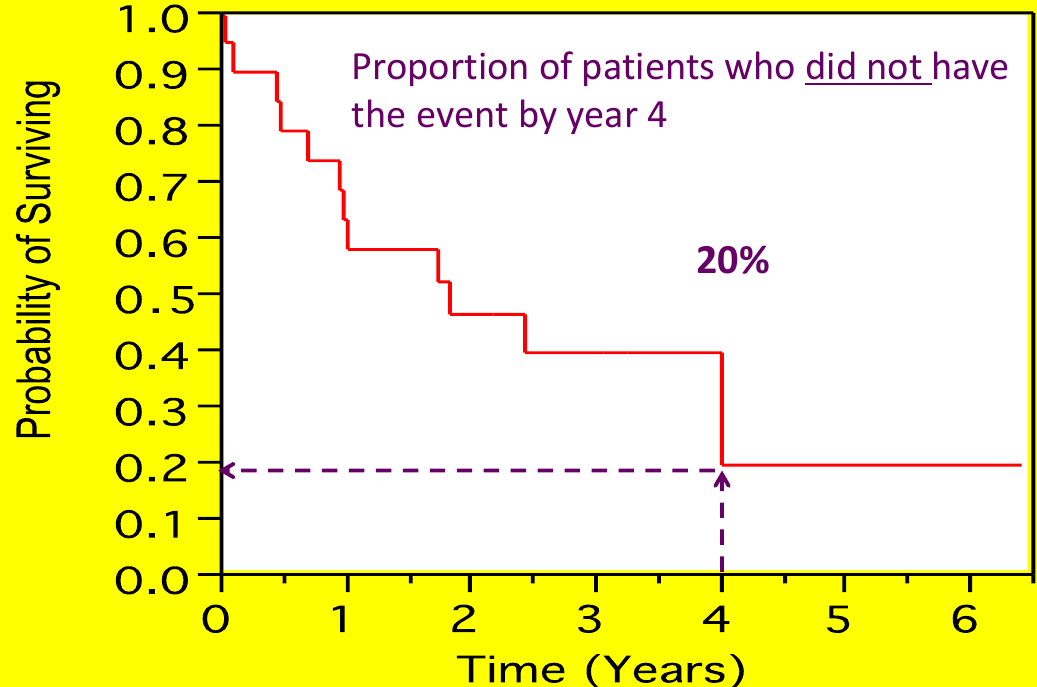
Each step is an "event", but cesnroing events are often marked as an 'X' (no step)

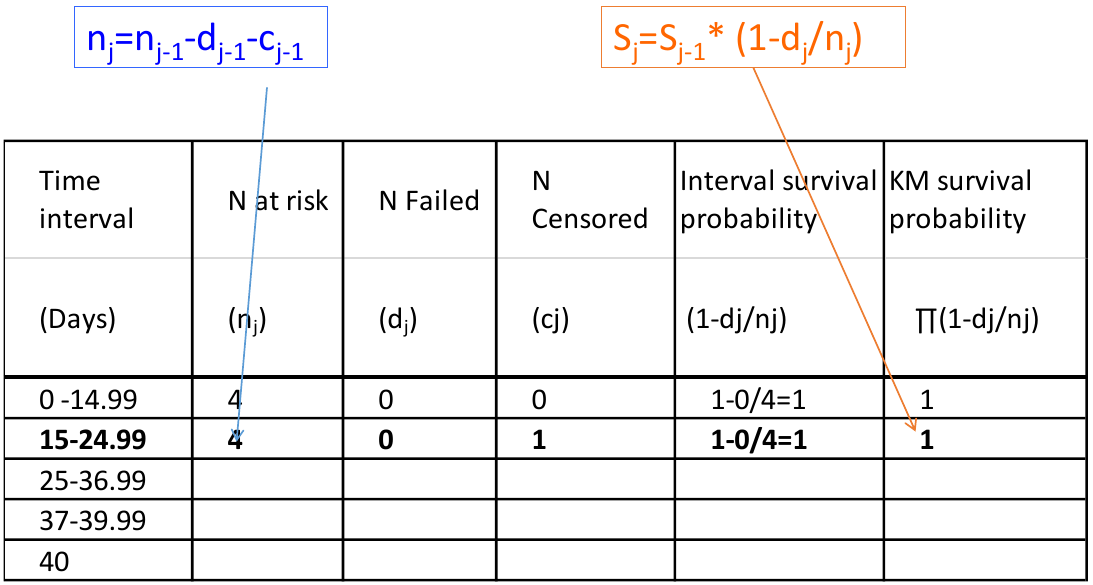
The most commonly used method for estimation of the survival function is the Kaplan-Meier (or product-limit estimator). Suppose there are k distinct event times and n subjects at risk of event, with d_j subjects with outcome at time t_j: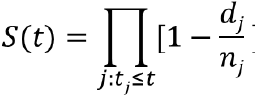

Kaplan-Meier estimates are calculated from the conditional probability of experiencing the event.