Sampling

In the practical use of statistics, we don't have an infinite amount of data. An enormous amount of data is needed to accurately estimate the true distribution non-parametrically. We need to take small samples of data, from which we can make inferences about the population from. We often describe this sample as empirical, originating or based on observation.

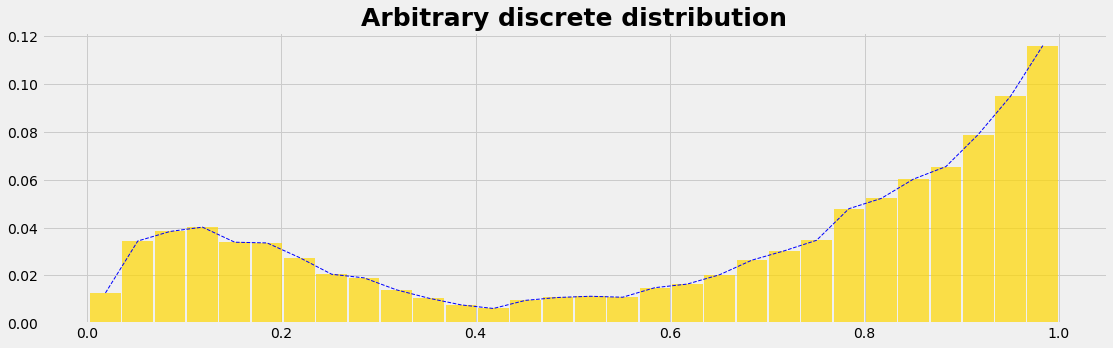
We model the quantity of interest as a random variable that follows some arbitrary probability distribution. In the case of discrete random variables, the probability distribution is characterized by probability mass functions (PMFs). Continuous random variables are represented by probability density functions (PDF). The area under the PMF and PDF curve is always equal to 1.

Let's assume we have a dataset we wish to use as a sampling engine. We'll assume the data:

• is Empirical
• is Discrete (given by data points)
• has an unknown function defining the distribution

If we want a random number generator that returns data with the same distribution of our empirical distribution we can do so in 3 steps:

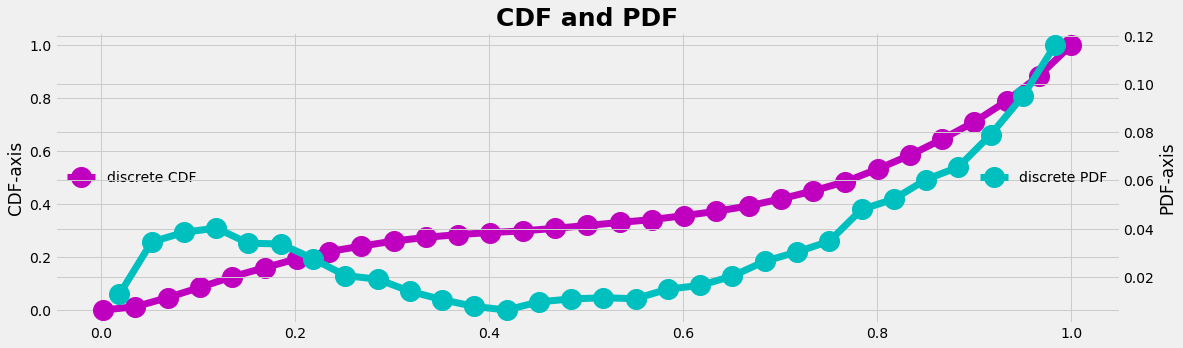
1. Define a cumulative density function (CDF) for our empirical distribution (the cumulative sum from the PDF, ranging from [0,1] on the y-axis)
2. Create a uniform random generator that gives data in the interval [0,1] 
3. Identify which element of the CDF the random number fits best and count the 'hit' (which is the x-axis transformation)

References

How to randomly sample your empirical arbitrary distribution