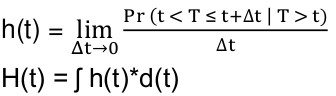Skip to main content

Survival Analysis I

Survival analysis is a measure of time until an event occurs. It doesn't only measure death as an outcome, and can adjust for covariates just as a logistic regression. But while a logistic regression only requires knowledge of whether an outcome occurred, survival analysis requires knowledge of the time until the outcome occurred.

This is usually used in a longitudinal cohort study; not common in case control studies as there is no accurate time information.

Survival Data

Survival data contains: entry time, whether the person had the event (dichotomous), and the time between when the person had the event or was last known to be event-free; as well as any other covariates (race, gender, age, etc).

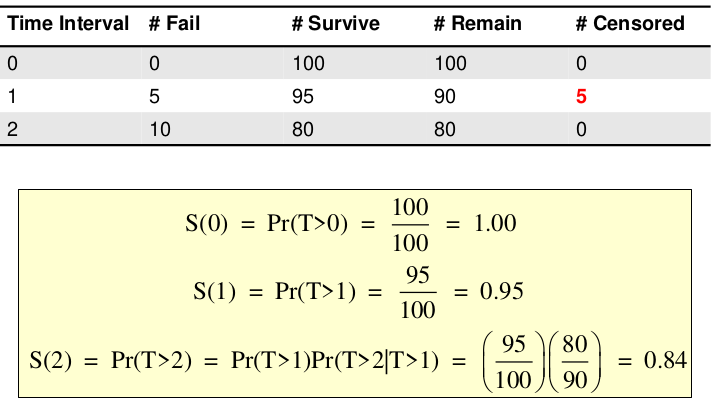
Even those who drop out of the study before the outcome occurs can provide information to the study. They are assumed to have the same likelihood of death as subjects with similar characteristics who survived at least the same amount of time.

Censoring

Censoring is removing a subject before we can measure the outcome.

Type I Censoring: Observations censored after some fixed length of follow-up.
Type II Censoring: Observations censored after a fixed percentage of subjects have the event of interest.
Random Censoring: Observations censored for reasons outside the control of investigators (e.g. drop-outs).
Informative Censoring: People censored that would have had different outcomes as people who remained in the analysis for the same amount of time.
Non-informative Censoring: People censored who would have had similar risk for the outcome as people who remained in the analysis for the same amount of time. Basic survival analysis assumes that censoring is non-informative.
Right-Censored: Lower limit on the time to an event for censored subjects (more common)
Left-Censored: An upper limit on time to event (less common, also called interval-censored with both upper and lower limits)

Survival Analysis vs. Alternatives

Linear Regression

If we have a continuous dependent variable, there are several issues with using a linear regression with time to event or censoring as outcome:

  • Censored observations can't be incorporated
  • Distribution of survival time is usually highly skewed since some people nearly always survive a long time
  • Disease status can't be handled
Logistic Regression

Neither time to event nor censoring are relevant in a logistic regression; the time between exposure and outcome is very short, and people cannot "drop out" of the study since they are recruited after the outcome is known.

Survival Function and Properties

Measures: Let T = survival time to event

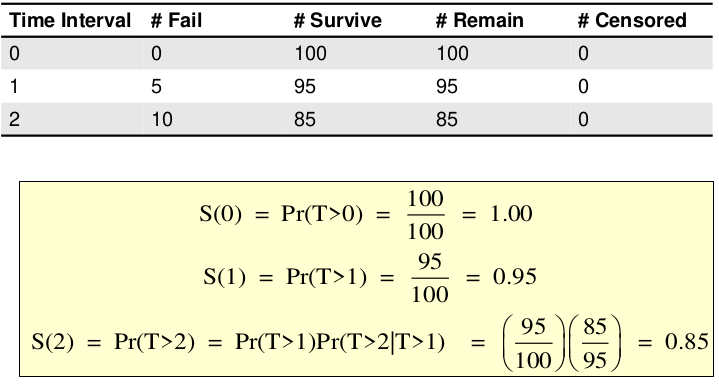
Survival probability:   S(t) = Pr (T > t) = Pr(the probability that an event has NOT occurred until time 't')

  • S(t=0) = 1 (all survive at the start)
  • S(t=inf) = 0 (non-one survives at infinity time)
  • 0 <= S(t) <= 1
  • S(t) is non-increasing function S(t1) >= S(t2) for t1 <= t2
Failure Function

T = survival time to event
Failure probability - the probability that event occurred by time 't'
F(t) = Pr(T <= t)

Relationship between survival function and failure function S(t) = 1 - F(t)

Hazard Rate

Instantaneous failure rate
image-1666624903180.png

Relationship between hazard and survival functions:
image-1666624941506.png

Cumulative hazard = H(t) = -ln(S(t))

Kaplan-Meier Curves

Kaplan-Meier curves (AKA Product-Limit Estimate) is a non-parametric approach. No assumptions on shape of the underlying distribution for survival time.

Example with censoring:image-1666625755914.png

Example with censoring:image-1666625788841.png

Summary Measures
  • Median survival - smallest survival time for which S(t) < .5
    • Sometimes this cannot be estimated
  • Mean survival
    • Often biased
  • Hazard Ratio - cannot be estimated from the KM curve and it depends on the proportional hazards assumption

Log-Rank Test

A crude comparison among several groups. Test whether two survival curves are statistically different by comparing observed events with expected events under the null hypothesis of no difference.

Back to top