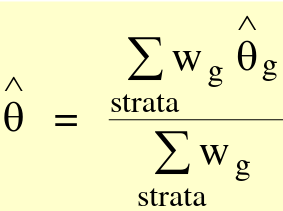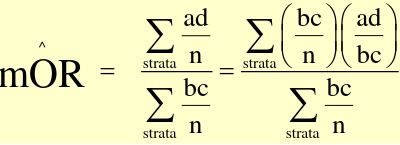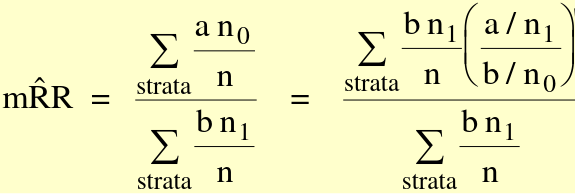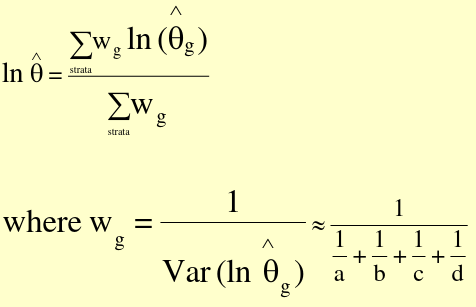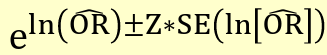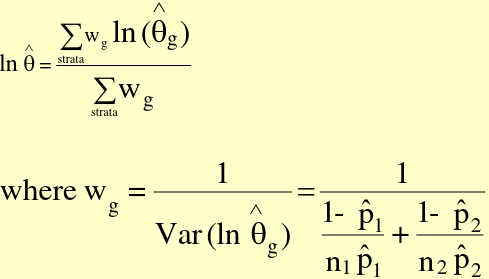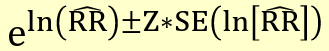Stratification and Interaction
Which Summary Measure to Use?
- Weighted averages are usually best
- Mantel-Haenszel is easy to compute and can handle zeros
- MLE measures are difficult and typically require a computer
Weighted Average in MH Summaries
Consider the following table:
| Sample 1 |
Sample 2 |
|
| n |
30 |
70 |
| x_bar |
5 |
8 |
Weighted average of population -> ((30*5)+(70*8))/(30+70) = 7.1
The average mean is closer to the cohort with a larger sample size. We can calculate any weighted average with the general form:
Where theta_hat is an estimator, such as mean or OR.
The MH Odds Ratio and RR can be described as weighted averages:
Where the weights are (b*c)/n
Where (a/n_1) / (b/n_0) is the risk ratio in each stratum, (b*n_1 / n) is the weight
Assumptions of Mantel-Haenszel Summary Measures
- Observations are independent from each other
- All observations are identically distributed
- The common effect assumption should hold:
- Follow-up cohort study - The stratum-specific risk ratios are all equal across the strata
- Case-control - The stratum specific odds ratios are all equal across the strata
MH measures are biased if the correctness of the common effect assumptions cannot be justified.
An extreme example: When interaction exists with protective and detrimental effects across strata; Protective effects negative in numerator in a stratum, and detrimental effects positive in numerator in another stratum.
Precision-based Summary Estimators
Also called Woolf's Method. Precision-based summary estimators are also weighted averages. Weighing each stratum according to its sampling error gives the most weight to the strata with the smallest variance. Precision-based are designed to have the greatest precision (smallest standard error). For Ratios we often take the log scale for a more symmetrical distribution. The general approach:
This is the sum of the products of each stratum-specific ratio times its weight, all divided by the sum of weights.
Precision-based Summary Odds Ratio
Thus, Var(ln(OR_hat) ~ 1/a + 1/b + 1/c + 1/d
And for CI:
Precision-based Summary Risk Ratio
Thus the Var(ln(RR_hat)) = ((1-p_hat1)/(n_1*p_hat1) + (1 - p_hat2)/(n_2*p_hat2))
And for CI: