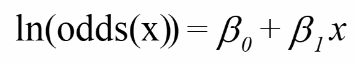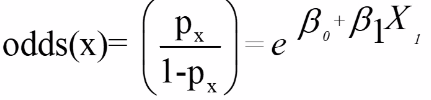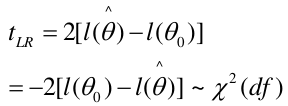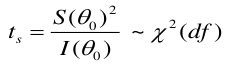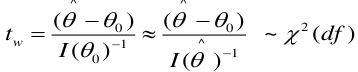Logistic Regression

Stratified analysis can be used to adjust for confounding, but the results can be difficult to adjust multiple confounders. If we have too many strata, we could end up with very small tables or 0 counts for some cells. WEWe can instead use Logistic Regression when the following situation exists:

The design is cross-sectional, case-control, cohort, or clinical trial
The outcome (D) is dichotomous
Any type of exposure (continuous, categorical or ordinal)
Confounders/covariates can be continuous, categorical or ordinal

Goals of Logistic Regression

Association: Between an outcome and a set of independent variables
Prediction: What do we expect the probability of outcome to be given the set of independent variables?
Exploratory: What variables are associated with outcome?
Adjustment for Confounding: Focus on a particular relationship; the other variables in the model are there for adjustment

Properties of Exponential and Logarithmic Functions

y = exp(x) -> log(y) = x

exp(x)*exp(z) = exp(x + z)

exp(x)/exp(z) = exp(x - z)

log(a*b) = log(a) * log(b)

log(a/b) = log(a) - log(b)

Logistic Regression Model

We assume a linear relationship between the predictor variable(s) and the Log-odds of an event that Y = 1:

~~For~~Thus, for risk p (if the design is ~~appropriate:~~appropriate):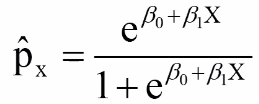

The predicted value of p is always between 0 and 1 and has a S-shaped curve.

Properties of Logistic Model with 1 Predictor: Case-Control Study

The log odds should be a straight line as given by: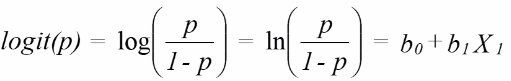

So if we have a X variable that is either 1 or 0 then the model would be:
logit(p | x = 0) = b₀ or log(p | x = 1) = b₀ + b₁*1

With E being exposure and bar(E) being non-exposure, we can define the odds ratio as: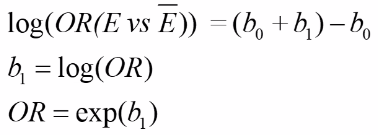
This represents the odds or log odds of developing disease with a dependent variable with one predictor in a case-control study.

This will also hold true for more than one covariate in the model. But this is not true for the RR.

Testing the Model

Two levels of testing:

Test of the model

Test of specific variables in the model

Likelihood Ratio Test

We can use the Maximum Likelihood test to estimate coefficients. Improvements in the likelihood by using the model with covariate instead of just the intercept. We use the Likelihood Ratio (LR) test when we do not know the distribution of LR.

H0: Model is x;
Ha: Model is x + all parameters

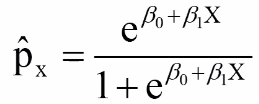
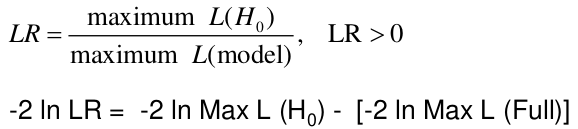
-2 ln(LR) has a chi-squared distribution with df = difference in number of parameters in the null and full models, assuming a large sample.

The LR, Wald, and Score test all measure the same hypothesis. For large sample sizes, they should all be equivalent. For small sample sizes LR is preferred.

LR test:

Score test:

Wald test: