Skip to main content

Interactions in Genetic Assocation Analysis

Statistical interaction occurs between two factors if their combined effect is different than what would be expected based on their individual separate effects. In genetics, differences in risk or mean phenotype between genotypes vary according to the exposure (interacting) variable.

Simple example: Phenylketonuria (PKU) is a genetic defect that causes severe intellectual disability only in the presence of dietary phenylalalnine. Every baby is tested for this trait to see if they need a special diet.

Modeling Statistical Interaction

We need a model to form an expectation for the joint effect, which we can use to define the interaction. The definition of interaction relies on some specification of non-interactive effects.

Let Gi be the genotype for person i, and Ei be an environmental factor for a person i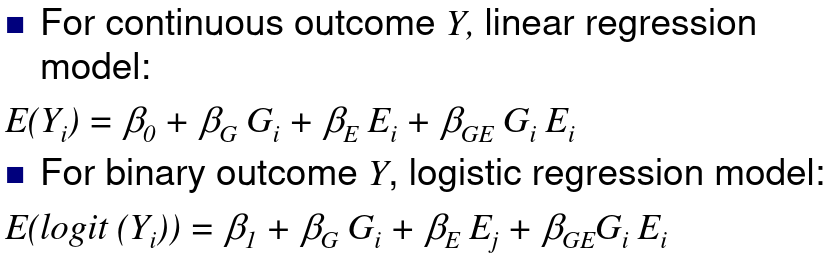
image-1669735373721.png

H0: βGE = 0; No interaction, the measure of association βG between the distribution of the phenotype Y and the genotype G does not depend on E.

  • Model interaction is always written as a departure from additive effects
  • For both logistic and linear regression, this translates to departure from additivity of effects
  • For logistic regression
    • Interaction == departure from additivity of log(ORs)
    • This is the same as departure from multiplicative OR effects
    • Interaction in logistic model is mutiplicaative interaction on the scale of the odds ratio
      • OR GE != ORg*ORE
      • ORG,E=1 != ORG,E=0

Example logistic model with interaction (CP = cleft palate):
image-1669740889941.png

So there are 2 interpretations of βGE:
1. The difference between the Environment logOR when G = 1 vs when G = 0
2. The difference between the Genotype logOR when E = 1 vs when E = 0

  • Overall we define βGE is the difference between the observed ln(OR) and the ln(OR) expected when the G and E act additively
  • When βGE = 0  (exp(βGE) = 1):
    • no departure from additivity
    • the genotypic OR in the two groups E = 1 and E = 0 are the same
    • the environment odds ratios in the two groups G = 1 and G = 0 are the same

If there is interaction, we should not use summary measures (OR & genotypic means) for the marker or the environmental factor alone. We may improve power to identify genes and SNPs by testing within subgroups of the interacting exposure, or just testing for interaction. 

Detecting Interactions: Power

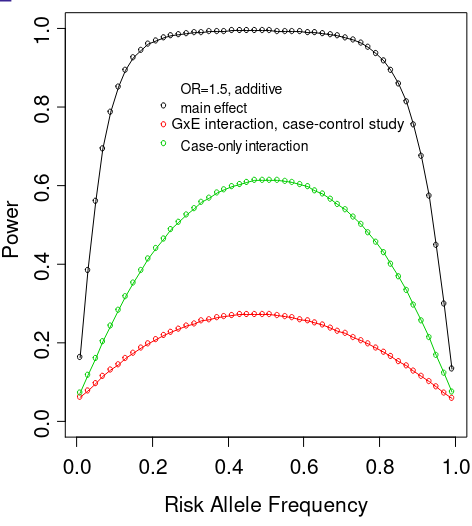
Even in the GWAS era, there are very few well-known examples of interaction of GxE that have been identified. This is in part due to the fact that tests for interaction are not as powerful as tests for main effect association.

We need much larger sample sizes to detect interaction than main effects, at least 4x the size is needed for same effect. Due to lack of power published reports of GxE interactions may be more prone to publication bias (although usually interaction is not the primary hypothesis in a study). It is better to publish all results to avoid publication bias, but this also leads to many published interactions that have not been replicated.

This power issue is particularly a problem when a large number of markers are tested; as always multiple testing adjustment is required to preserve family-wise error rate. We'll focus on two strategies for maximizing power when conducting GxE GWAS have been proposed: Case-only designs and two-stage screening procedures

Case-Only Design

If G and E are independent (depending on design, in population or among controls) cases from a case-control study can be used to estimate the multiplicative GxE interaction.

When G and E are independent in the controls, the OR for the G-E association among cases equals the multiplicative interaction between E and G. ??Improved precision: acts like a case-control or cohort study with an infinite number of controls.??

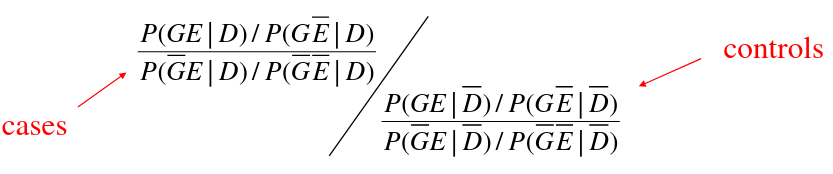
image-1669742387338.png
The interaction OR is the ratio of G-E OR in cases to G-E OR in controls.

If G and E are independent in the controls then the joint probability P(GE | D) = P(G | D)*P(E | D) and the ratio of ORs is just the E-G OR among cases.

We can test for G-E interaction by looking at the G-E association in cases.

Advantages
  • Can be inexpensive for exploratory analyses
  • Useful for case tissue specimens archived from earlier studies
  • Power for the case-only interaction test is much greater than for interaction test in case-control study with same number of cases
  • When independence assumption is met, case-only design is much more powerful than case-control logistic regression test of interaction

    image-1669742986286.png

Limitations
  • Provides non information about main effects
  • The interaction estimate can be biased if the assumption of G-E independence is violated

Two-Stage Screening Procedure

A screening procedure gives us a way to select only a small subset of the SNPs m << M to test for G-E interaction. Slide 45

Back to top