Skip to main content

Tree Based Methods

Classification and regression trees can be generated from multivariable data sets using recursive partitioning with:

  • Gini index or entropy for a categorical outcome
  • Residual sum of squares for a continuous outcome

We can use cross-validation to assess the predictive accuracy of tree-based models.

Non-Linear Regression

Polynomial Regression adds extra predictors by raising original predictors to a power. Provides a simple way to provide a nonlinear fit to data.

Step functions/Broken stick regression cuts the range of a variable into K distinct regions. Fits a piecewise constant function/regression line.

Regression splines and smoothing lines is an extension of the two above. The range of X is divided into K distinct regions. Within each region a polynomial function is fit to the data. It is constrained in a way which smoothly joins at the region boundaries, or knots. It can produce an extremely flexible fit if there are enough divisions.

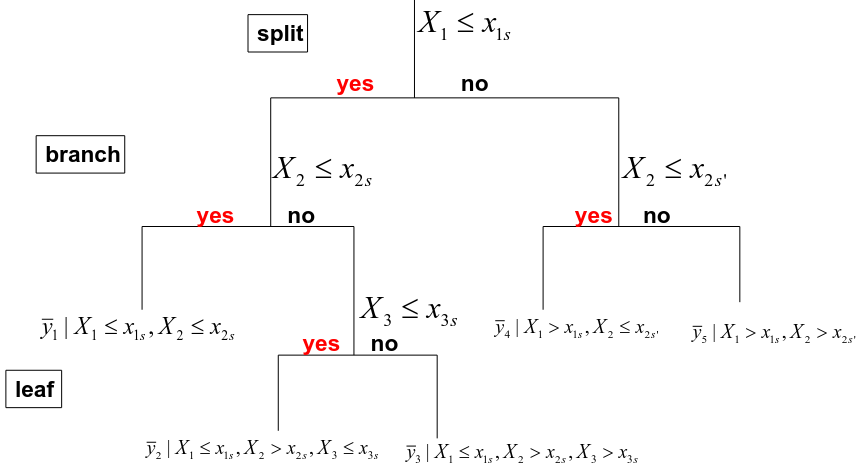
CART: Classification and Regression Trees

CART are a computer intensive alternative to fitting classical regression models.

  • These involve stratifying or segmenting the predictor space into a number of simple regions.
  • In order to make a prediction for a given observation we typically use the mean or mode of the training observations in the region which it belongs to.
  • Classification trees apply when the response it categorical
  • Regression trees apply when the response is continuous

Building a Regression Tree

image-1666304260933.png

  1. We divide the predictor space into J distinct and non-overlapping regions R1, R2, RJ.
  2. The fitted value in a region Rj is simply the mean of the response values in this region :

    image-1666304470132.png

Goal: The regions are identified to minimize:

image-1666304497649.png
A copmlete search is not feasible and we take a top-down, greedy approach known as recursive binary splitting.
Top-down: Start from the top of the tree
Greedy: Best solution at each node of the tree (local rather than global)

Recursive Binary Splitting

Input: "explainatory" variables and outcome Y

For each variable Xg,
without splitting Xg, the variable Y has a certain variabilityimage-1666304720370.png

 

 

Back to top