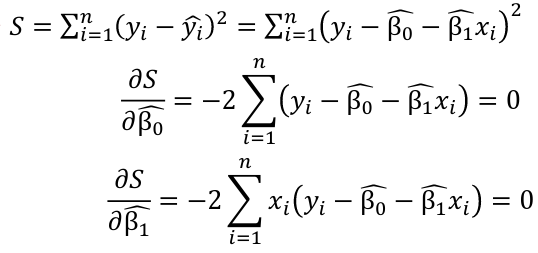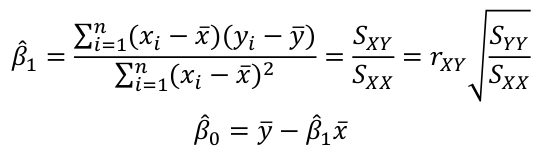Simple Linear Regression
One of the first known uses of regression was to study inheritance of traits from generation to generation in a study in the UK from 1893-1898. E.S. Pearson organized the collection of heights of mothers and one of their adult daughters over 18. The mother's height was the predictor variable (x) and the daughter's height was the response variable (y).
The goal of a linear regression is to quantify the relationship between one independent variable and a single dependent variable. A simple linear regression can be represented by the following:
- y = β0 + β1x + Error; E(Error) = 0; V(Error) = σ2
- E(y) = β0 + β1x ; V(y) = σ2
As with correlation, a strong association in a regression analysis does NOT imply causality
How to find the best line?
OLS/LS - Ordinary Least Squares is a method that looks for the line that minimizes the "residual sum of squares"
Residual = Observed - Predicted = y - ŷ
So we can set up an equation for sum of squared residuals and take the derivative, set to zero, and solve.
The solution comes out to:
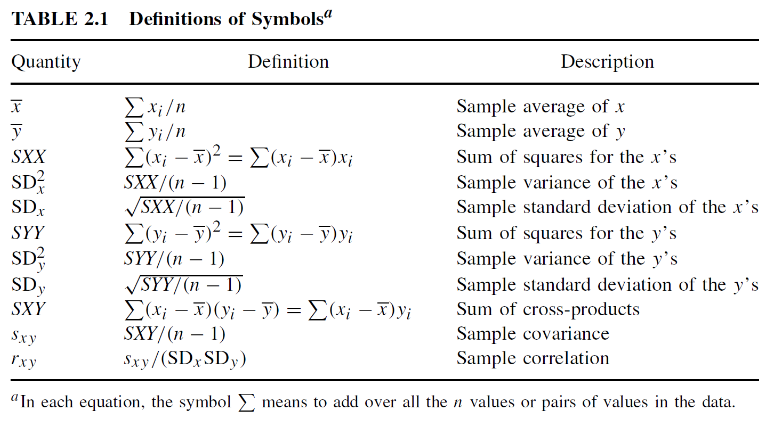
Notations commonly seen in our textbook: