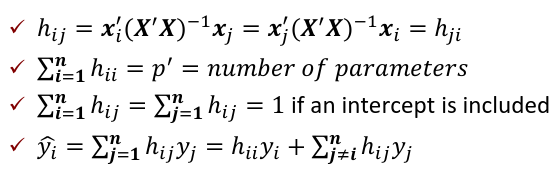Skip to main content

Regression Diagnostics

The estimation and inference from the regression model depends on several assumptions. These assumptions need to be checked using regression diagnostics.

We divide the potential problems into three categories:

  • Error: 𝜀 ~ N(0, 𝜎2I); i.e. the errors are:
    • Independent
    • Have equal variance
    • Are normally distributed
  • Model: The structure part of model E[y] = Xβ is correct
  • Unusual observations: Sometimes just a few observations do not fit the model but might change the choice and fit of the model
Diagnostic Techniques
  • Graphical
    • More flexible but harder to definitively interpret
  • Numerical
    • Narrower in scope but require no intution

Model building is often an interactive and interactive process. It is quite common to repeat the diagnostics on a succession of models.

Unobservable Random Errors

Recall a basic multiple linear regression model is given by:
    E[Y|X] = Xβ   and   Var(Y|X) = 𝜎2I

The vectors of errors is 𝜀 = Y - E(Y|X) = Y - Xβ; where  𝜀  is unobservable random variables with:
    E(𝜀 | X) = 0
    Var(𝜀 | X) =  𝜎2I

We estimate beta with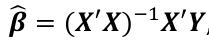
image-1665094586198.png
and the fitted values Y_hat corresponding to the observed value Y are: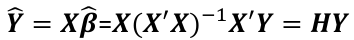image-1665094623407.png
Where H is the hat matrix. Defined as: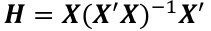
image-1665094651063.png

The Residuals

The vector of residuals e_hat, which can be graphed, is defined as: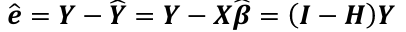image-1665094692646.png
    E(e_hat | X) = 0
    Var(e_hat | X) = 𝜎2(I - H)
    Var(e_hat_i | X) = 𝜎2(I - hii); where hii is the ith diagonal element of H.

Diagnostic procedures are based on the residuals which we would like to assume behave as the unobservable errors would.

Cases with large values of hii will have small values for Var(e_hat_i | X)

The Hat Matrix

The hat matrix H is n x n symmetric matrix

  • HX = X
  • (I - H)X = 0
  • HH = H2 = H
  • Cov(Y_hat, e_hat | X) = Cov(HY, (I - H)Y| X) =  𝜎2H(I - H) = 0

image-1665095127938.png

hii is also called the leverage of the ithith case. As hii approaches 1, y_hat_i gets close to y_i.

Error Assumptions

We wish to check the independence, constant variance, and normality of the errors  𝜀. The errors are not observable, but we can examine the residuals e_hat.

They are NOT interchangeable with the error.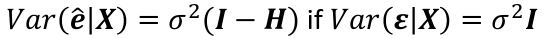image-1665095273422.png

The errors may have equal variance and be uncorrelated while the residuals do not. The impact of this is usually small and diagnostics are often applied to the residuals in order to check the assumptions on the error.

Constant Variance

Check whether the variance in the residuals is related to some other quantity Y_hat and Xi

  • e_hat against Y_hat: If all is well there should be constant variance in the vertical direction (e_hat) and the scatter should be symmetric vertically about 0 (linearity)
  • e_hat against Xi (for predictors that are both in and out of the model): Look for the same things except in the case of plots against predictors not in the model, look for any relationship that might indicate that this predictor should be included.
  • Although the interpretation of the plot may be ambiguous, one can be at least sure that nothing is seriously wrong with the assumptions.

Normality Assumptions

The tests and confidence intervals we used are based on the assumption of normal errors. The residuals can be assessed for normality using a QQ plot. This compares residuals to "ideal" normal observations.

Suppose we have a sample of n: x1, x2... xn. and wish to examine whether the x's are a sample from normal  distribution:

  • Order the x's to get x(1) <= x(2).... <= x(n)
  • Consider a standard normal sample of size n. Let z(1) <= z(2).... <= z(n)
  • If x's are normal then E[x(i)] = mean + sd*z(i); so the regression of x(i) on z(i) will be a straight line

Many statistics have been proposed for testing a sample for normality. One of these that works well is the Shapiro and Wilk W statistic, which is the square of the correlation between the observed order statistics and the expected order statistics.

  • H0 is that the residuals are normal
  • Only recommend this in conjunction with a QQ plot
  • For a small sample size, formal tests lack power
  • For a large dataset, even mild deviations from non-normality may be detected. But there would be little reason to abandon least squares because the effects of non-normality are mitigated by large sample sizes.

Testing for Curvature

One helpful test looks for curvature in the plot. Suppose we have residual e_hat vs a quantity U where U could be a regressor or a combination of regressors.

A simple test for curvature is:

  • To refit the model with an additional regressor for U^2 added
  • The test is based on test testing the coefficient for U^2 to be 0
  • If U does not depend on estimated coefficients, then a usual t-test of this hypothesis can be used
  • If U is equal to the fitted values (which depends on the estimated coefficients) then the test statistic is approximately the standard normal distribution

Code

## Test for normallity
gs <- lm(sqrt(Species) ~ Area + Elevation + Scruz + Nearest + Adjacent, gala)
g <- lm(Species ~ Area + Elevation + Scruz + Nearest + Adjacent, gala)

par(mfrow=c(2,2))
plot(fitted(g), residuals(g), xlab="fitted", ylab="Residuals")

qqnorm(residuals(g), ylab="Residuals")
qqline(residuals(g))

hist(g$residuals)

## Testing for curvature
library(alr4)
m2 <- lm(fertility ~ log(ppgdp) + pctUrban, UN11)
residualPlots(m2)
summary(m2)$coeff
Back to top