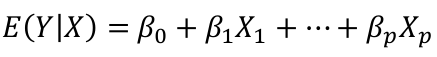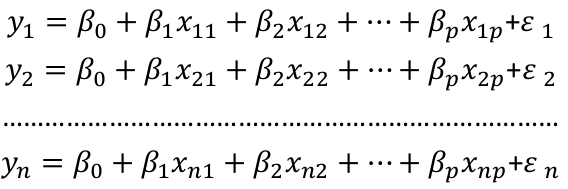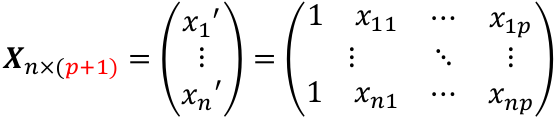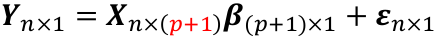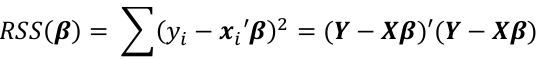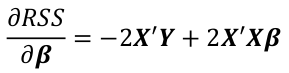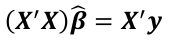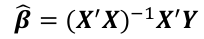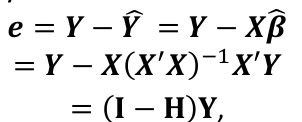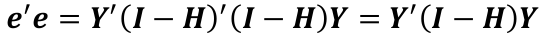Mutiple Linear Regression and Estimation

Multiple Linear Regression analysis can be looked upon as an extension of simple linear regression analysis to the situation in which more than one independent variables must be considered.

The general model with response Y and regressors X₁, X₂,... X_p:

Suppose we observe data for n subjects with p variables. The data might be presented in a matrix or table like:

We could then write the model as:

We can think of Y and E as (n x 1) vectors when transposed, and β as a ((p + 1) x 1) vector. p +1 is number of predictors + the intercept. Thus X would be:

Rhe general linear regression may be written as:

Or y_i = x_i^|*β + ∈_i

The model is represented as the systematic structure plus the random variation with n dimensions = (p + 1) + { n - (p + 1 ) }

Ordinal Least Squares Estimators

The least squares estimate β_hat of β is chosen by minimizing the residual sum of squares function:

By differentiating with respect to β_i and solve by setting equal to 0:

The least squares estimate of β_hat of β is given by:

and if the inverse exists:

Fitted Values and Residuals

The fitted values are represetned by Y_hat = X*β_hat

where the hat matrix is defined as H = X(X^|X)^-1X^|

The residual sum of squares (RSS):

Gauss-Markov Conditions

In order for estimates of β to have some desirable statistical properties, we need a set of assumptions referred to as the Gauss-Markov conditions; for all i, j = 1... n

E[∈_i] = 0
E[∈_i²] = 𝜎²
E[∈_i∈_j] = 0, where i != j

Or we can write these in matrix notation as: E[∈] = 0, E[∈∈^|] = 𝜎²*I

The GM conditions imply that E[Y] = Xβ and cov(Y) = E[(Y-Xβ)(Y-Xβ)^|] = E[∈∈^|] = ∈