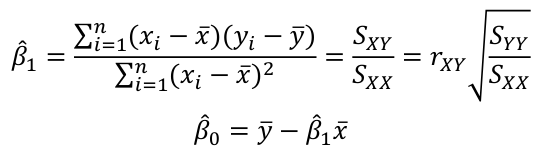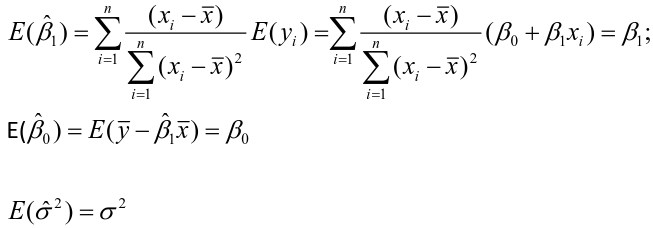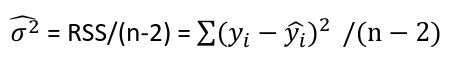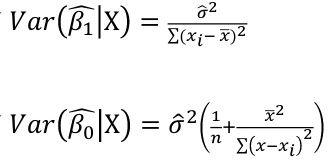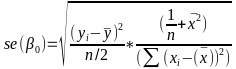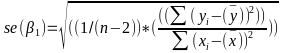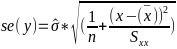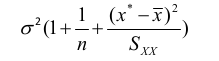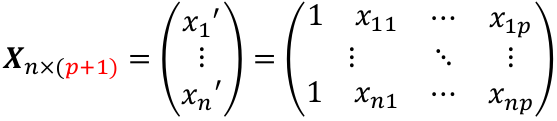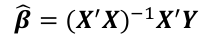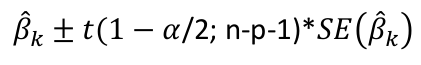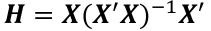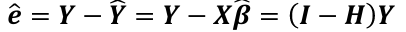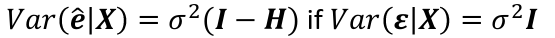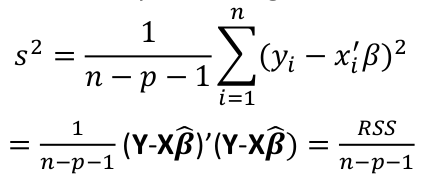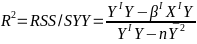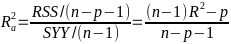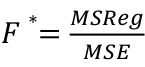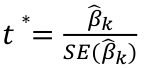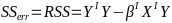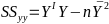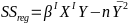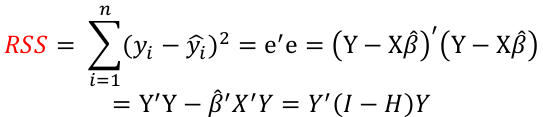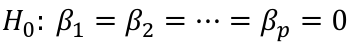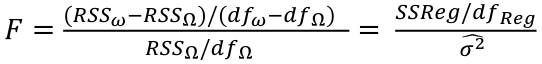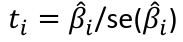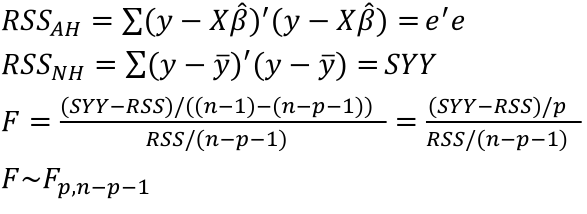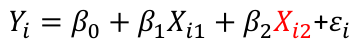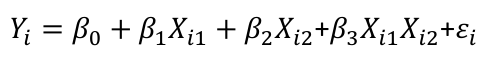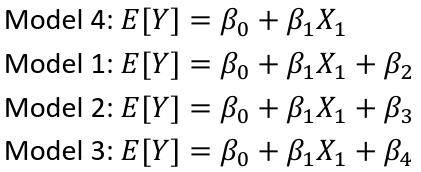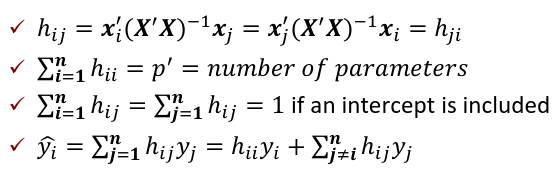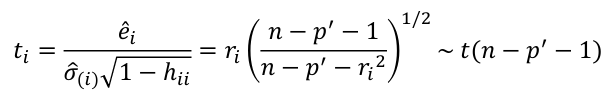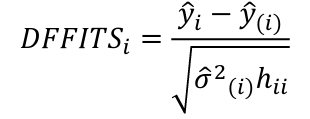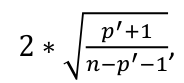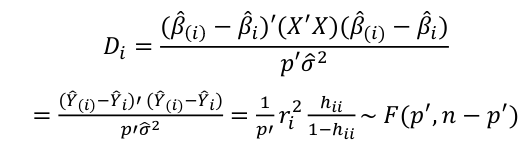Midterm Cheat Sheet

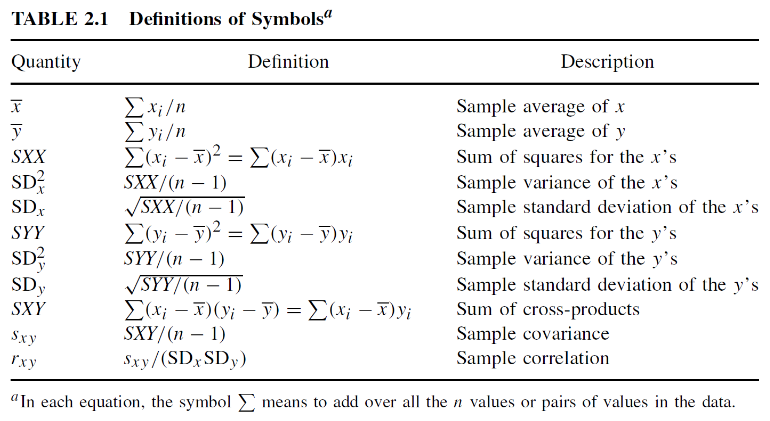
Linear Regression

Predicting a CI new obs adds a 1 to se(y):

𝛽₀ + 𝛽₂x +/-

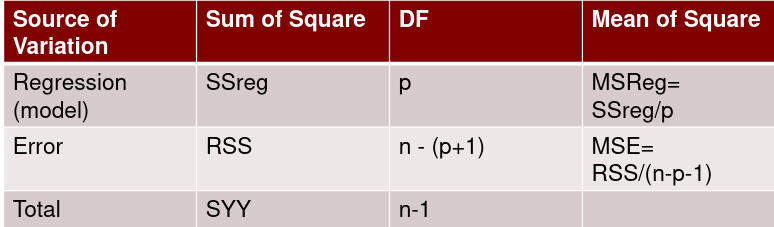
Multiple Linear Regression and Estimation

𝐻0 : 𝛽1 = 𝛽2 = 𝛽3 = ⋯ = 𝛽𝑝 = 0  
v.s.  𝐻1 : not all 𝛽𝑘 = 0, 𝑘 = 1, … , 𝑝

rejection rule of 𝑡 >= t(1 − alpha/2; 𝑛 − 𝑝 − 1)

Model Fitting: Inference

df_Ω = n - p, and df_𝜔 = n – q

Reject the null hypothesis if F > Fα p - q, n – p

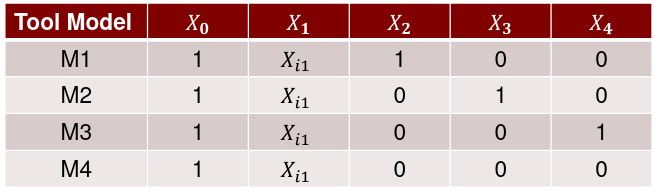
Dummy Variables and Analysis of Covariance
Consider a Xi2 for which is 0 for – and 1 for +:

An interaction between Xi1 and Xi2:

A model with multiple categorical variables:

Regression Diagnostics
Assumptions:
    • Error:  ~ N(0, SD2I); 
        ◦ Independent
        ◦ Equal Variance
        ◦ Normally Distributed
    • Model: E[y] = Xβ is correct
    • Unusual observations
      
Leverage Points: data point with unusual x-value

      The Hat Matrix – n*n matrix
hii is the leverage of the ith case
leverage > 2p’/n should be looked at closely

Outliers: Unusual observation on x or y axis

Calculate the t-test and compare abs with limit:
abs(qt(.05/(n*2), df = n - pprime - 1, lower.tail = T))

Influential Points: causes changes to regression
    Difference in Fits:

with a threshold of

Where p’ is the number of parameters 

    Cook's Distance:

with a threshold of
Di > 4/n should be looked at
Di > .5 possible influence
Di >= 1 very influential

Error: a plot of e_hat should
    • have constant variance
    • have no clear pattern
    • H0: residuals are normal