Intro to Cluster Analysis

Clutsering refers to a very broad set of techniques for finding subgroups, or clusters, in a data set. When we cluster the observations, we partition the profiles into distinct groups so that the profiles are similar within the groups but different from other groups. To do this, we must define what makes observations similar or different.

PCA vs Clustering

Both clustering and PCA seek to simplify the data via a small number of summaries, but their mechanisms are different:

• PCA searches for a low-dimensional representation of the observations that explains a good fraction of the variance
• Clustering looks to find homogeneous subgroup among the observations

Notation

Input is data with p variables and n subjects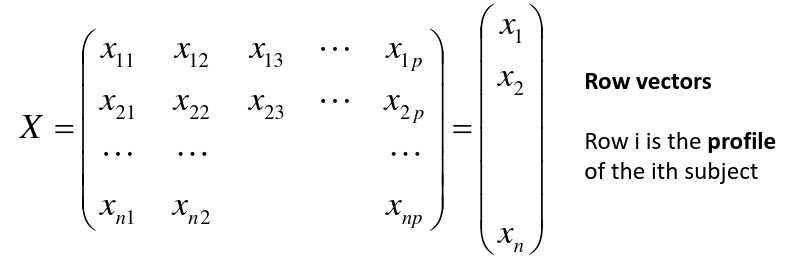

A distance between two vectors i and j must obey several rules:

• The distance must be positive definite, d_ij >= 0
• The distance must be symmetric, d_ij = d_ij, so that the distance from j to i is the same as the distance from i to j
• An object is zero distance from itself, d_ii  = 0
• The triangle rule - When considering three objects i, j and k the distance from i to k is always less than or equal to the sum of the distance from i to j and the distance from j to k
  d_ik <= d_ij + d_jk

Clustering Procedures

• Hierarchical clustering: Iteratively merges profiles into clusters using a simple search. Start with each profile/cluster and end with one 1. The clustering procedure is represented by a dendrogram.
• K-mean clustering: Start with a per-specified number of clusters and random allocation of profiles to clusters. Iteratively move profiles from one cluster to the other to optimize some criterion. End up with the same number of clusters.