Skip to main content

Introduction

Generalized linear models are extensions of classical linear models. Classes of generalized linear models include linear regression, logistic regression for binary and binomial data, nominal and ordinal multi-nomial logistic regression, Poisson regression for count data and Gamma regression for data with constant coefficient of variation.

Generalized Estimating Equations (GEE) provide an efficient method to analyze repeated measures where the normality assumption does not hold. 

In SAS there are > 10 procedures that will fit a linear regression, example:

title " Simple linear regression of Income " ;
proc reg data = IM ;
model Inc = EN Lit US5 ;
output out = OutIm ( keep = Nation LInc Inc En Lit US5 r lev cd dffit )
rstudent = r h = lev cookd = cd dffits = dffit ;
run ;
quit ;

A model generally fits well if the residuals,  or difference between predicted and observed, are small. The assumption of a linear model are primarily checked through the residuals (normality, homoscedasiticity/constant variance and linearity)

R-Squared is a measure of goodness-of-fit where higher values are indicative of a better fit.
      R2 = Explained Variation  /  Total Variation
The issue with R-Squared is that more predictors will increase R2 regardless of the quality of the predictor. R-Squared-Adjusted penalizes for complexity.

We do not want observations that lie on the '1%' ends of the distributions to influence the model. The leverage of an observation is defined in terms of its covariate values.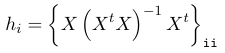
image.png
An observation with high leverage may or may not be influential;  Where we have p predictors and n observations we define leverage points as hi > 4/n
A point with high leverage might not have high influence, that is the model does not change substantially when the point is excluded. Cook's distance can be used to identify influential points: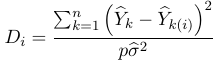
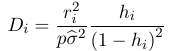
image.pngOR image.png
Other measures of the influence are:
DFFITTS, how much an observation has effected the fitted value: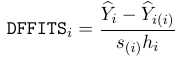
image.png
DFBETAS, the difference in each parameter estimate:  Values larger than 2/sqrt(n) should be investigated.

Back to top