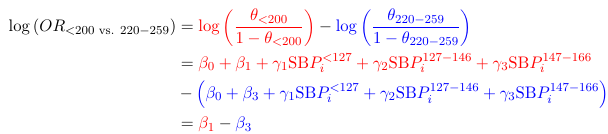Skip to main content

Hypothesis Testing with GLM

Effect modification can be modeled with logistic regression by including interaction terms. A significant interaction term implies a departure from heterogeneity between groups.

Consider the following example were we wish to compare admission rates by sex per department: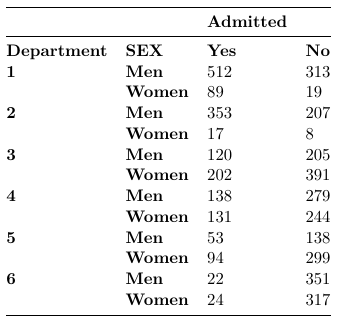
image.png
With summary of fit: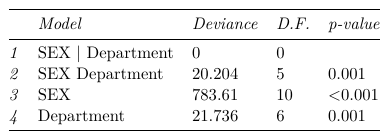
image.png
Which we observe only the saturated model fits the data well. To compare ORs across department we estimate the department specific odds from the saturated model:

ods select estimates ;
title1 ’ Estimated ODDS Ratio ( F vs M ) in each Department ’;
proc genmod data = one ;
class department SEX ;
model yes / total = SEX | department / link = logit dist = bin covb ;
estimate ’ SEX1 ’ SEX 1 -1 department * SEX 1 -1 0 0 0 0 0 0 0 0 0 0/exp;
estimate ’ SEX2 ’ SEX 1 -1 department * SEX 0 0 1 -1 0 0 0 0 0 0 0 0/exp;
estimate ’ SEX3 ’ SEX 1 -1 department * SEX 0 0 0 0 1 -1 0 0 0 0 0 0/exp;
estimate ’ SEX4 ’ SEX 1 -1 department * SEX 0 0 0 0 0 0 1 -1 0 0 0 0/exp;
estimate ’ SEX5 ’ SEX 1 -1 department * SEX 0 0 0 0 0 0 0 0 1 -1 0 0/exp;
estimate ’ SEX6 ’ SEX 1 -1 department * SEX 0 0 0 0 0 0 0 0 0 0 1 -1/exp;
run ;

The hypothesis tests we've encountered so far can be expressed in terms of linear combinations of the model parameters; However, other tests have to be carried out that may not be included in default output which requires a good understanding of the model.

For example, a few important properties we've seen so far:

  1. Differences between groups (Lecture 4)

    image.png

    Expressed as a linear combination:
        1 × β1 + 0 × β2 + (−1) × β3 + 0 × β4 = 0
  2. Independence in 2 way tables defines by categorical variables X and Y
    H0: X and Y are independent <-> H0: all λXYij = 0
    HA: X and Y are dependent <-> HA: at least one λXYij != 0

    Expressed as a linear combination:
        λ11 = λ12 = λ21 = λ22 = 0

        1 × λ11 + 0 × λ12 + 0 × λ21 + 0 × λ22 = 0
        0 × λ11 + 1 × λ12 + 0 × λ21 + 0 × λ22 = 0
        0 × λ11 + 0 × λ12 + 1 × λ21 + 0 × λ22 = 0
        0 × λ11 + 0 × λ12 + 0 × λ21 + 1 × λ22 = 0

  3. Significance of parameters (Lecture 4)

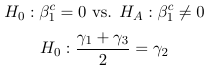
    image.png

    Expressed as a linear combination:
        (For ordinal SBP): 0 × β0c + 1 × β1c + 0 × β2c = 0
        (For SBP): γ1 + (−2) × γ2 + γ3 + 0 × γ4 = 0

In all cases the null hypothesis can be expressed as a linear combination of the parameters (this is important in understanding contrast and estimate statements in SAS).

Looking at ex. 1 above, we could test the null hypothesis with a t-test: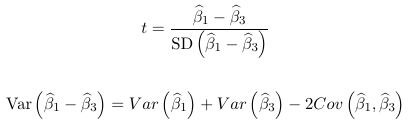
image.png
or the Wald test with w = t2. Only variances of coefficients are reported by default in PROC GENMOD, so to get the covariance matrix the covb option is needed in the model statement. But when we want to test more than one linear combination of parameters at the same time this becomes complex and time consuming to do manually.

In sas we use CONTRAST and ESTIMATE statements to carry out this type of test.

title1 ’ Contrasting <200 vs . 220 -259 with CONTRAST and ESTIMATE statements ’;
proc genmod data = CHD ;
class CHOL SBP ;
model CHD / Total = CHOL SBP / dist = Binomial link = logit ;
estimate ’ <200 vs . 220 -259 ’ CHOL 0 -1 1 0/ exp ;
contrast ’ <200 vs . 220 -259 ’ CHOL 0 -1 1 0;
run ;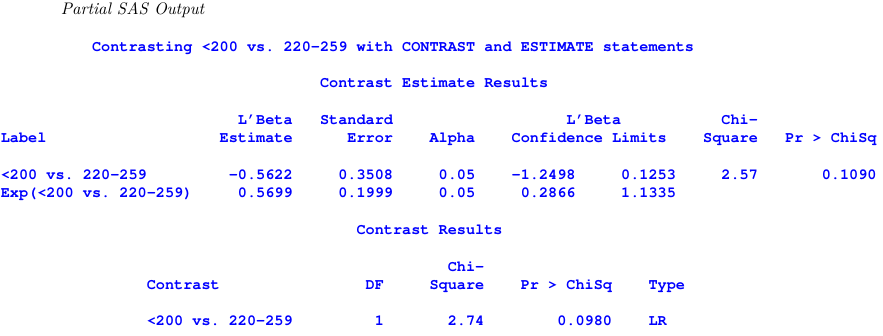

image.png
The chi-sqaure test statistic in the two tests is different because estimate uses a t-test while contrast uses a Wald test.

Back to top