Skip to main content

Introduction to Bayesian Modeling

In the frequentist approach, probabilities are estimated based on observed frequencies in available data. Bayesian analysis is based on expressing uncertainty about unknown quantities as formal probability distributions.

Bayes Problem: Given the number of times in which an unknown event has happened and failed - Requires the chance that the probability of its happening in a single trial lies somewhere between any two degrees of probability that can be named.

Bayesian statistics used probability as the only way to describe uncertainty in both data and parameter. Everything that is not known for certain are modeled with distributions and treated as random variables.


 Exposed
 Unexposed
Diseased
 a
 b
 m1
Not Diseased
 c
 d
 m0

n1
 n0
 n

Recall the odds ratio (OR) is the probability of having an outcome (disease) compared to the probability of not having the outcome: ad / bc

Bayesian Statistics takes the point of view that OR and RR are uncertain unobservable quantities.

Prior probability: Model/probability distribution using existing data/knowledge
Posterior probability: Updated model with new and prior data

Bayes theorem allows us to learn from experience and turn a prior distribution into a posterior distribution.

Bayes Theorem

P(H) = Probability of H
P(H | data) =( P(data | H)*P(H) ) / P(Data) = Posterior probability of H

image.png

Consider a generic probability distribution p(𝜃) for a single parameter 𝜃. The probability distributions are defined as:

image.png

Computer Simulation

There are several ways to calculate the properties of probability distributions for unknown parameters. We will be focusing on using simulation of the known random variables and estimate the property of interest.

Note that there are entire classes on algorithms used for simulation, we will not go into great depth on the underlying theory.

Monte Carlo Methods

Monte Carlo algorithms are a broad class of computational algorithms that rely on repeated random sampling to obtain numerical results.

Suppose we have a random variable X which has a probability distribution p(x) and we have an algorithm for generating a large number of independent trials x(1), x(2), ... x(T) . Then:

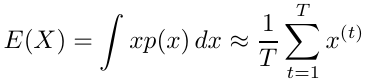image.pngBy the law of large numbers the approximation becomes exact as T approaches infinity.

In R:

# Step 1: Generate samples
x <- rbinom(1000, 8, 0.5)
# Represent histogram
hist(x, main = "")
# Step 2: Estimate P(X<=2) as
# Proportion of samples <= 2
sum(x <= 2)/1000
## 0.142

JAGS

The below code does the same thing using JAGS (in R):

library(rjags)
### model is defined as a string
model11.bug <- "model {
Y ~ dbin(0.5, 8)
P2 <- step(2 - Y)
}"
writeLines(model11.bug, "model11.txt")
# Now run the Gibbs sampling for 1000 iterations
### (Step 1) Compile BUGS model
M11 <- jags.model("model11.txt", n.chains = 1, n.adapt = 1000)
### (Step 2) Generate 1000 samples and discard
mcmc_11 <- update(M11, n.iter = 1000)
### (Step 3) Generate 10000 samples and retain for
### inference
test_11 <- coda.samples(M11, variable.names = c("P2", "Y"), n.iter = 10000)

Gibbs Sampling is MCMC algorithm that reduces high dimensional simulation to lower dimensional simulations. Used in BUGS and JAGS as the core algorithm for sampling from posterior distributions.

Back to top