Skip to main content

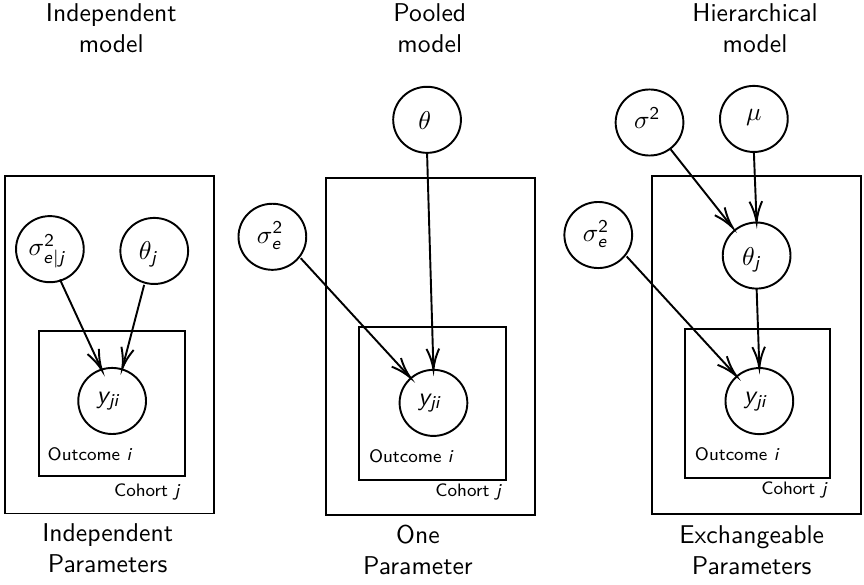
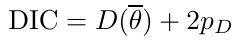Hierarchical Models

In Bayesian hierarchical models, we start by imposing a prior that is a function of different parameters. We'll introduce a new variable γ, which is called the hyper-prior; The prior of α depends on β, which depends on γ.
image.png

A typical example of this in medical research is population of hospitals, providers within hospitals, and patients within providers. Any datasets with such a structure are called hierarchical.

We are interested in making inference of specific units. In doing so observations may be collected over time on the same individuals, so repeated measures must be accounted for.

image.png

Ranking Posterior Estimates

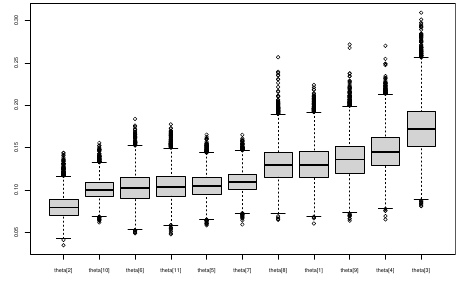
image.png
We can simply rank the outcome/results in a box plot such as the above, but this does not consider the uncertainty of the estimates.

We can derive the posterior distribution of each ranking by ranking the estimates at each iteration of the Gibbs Sampling and generate the posterior distributions of the ranks. Below the ranks are in parenthesis:
image.png
The posterior distribution of ranks gives us a measure of the uncertainty of the ordering.

Comparing Hierarchical Models

There are three primary approaches used:

  • Deviance Information Criterion (DIC)

    image.png
    Which is based on p(y | θ)

  • Akaike Information Criterion (AIC)
        AIC = -2 log(y | φ̂) + 2pφ
    where pφ is the number of hyperparameters
  • Bayesian Information Criterion (BIC)
        BIC = -2 log(y | φ̂) + log(n)*pφ

"Likelihood" is not well defined in a hierarchical model; It depends on the "focus" of the study if we want to use θ, φ, or the model structure without any unknown parameters. It is not a matter of which is correct but which is appropriate for our purpose.

Consider an example where our model predicts classes within schools in within a country:

  • If we are interested in predicting future classes in those school then θ is the focus and deviance-based methods such as DIC are appropriate
  • If we are interested in predicting results of future schools in a country then φ is the focus and marginal-likelihood methods such as AIC are appropriate; Relevant to education within the whole country.
  • If we are interested in predicting results for a new country, then no parameters are in focus, the Bayes factors are appropriate to compare models; Relevant to general statements about education in the
  • whole world or outside of the country being studied.


Back to top