Skip to main content

Bayesian Modeling - Logistic

Let Y be an indicator for presence of disease ->    Y | p ~ Bin(p, 1)

Logistic regression models the log-ODDS (also called logit) of the mean outcome using a linear predictor.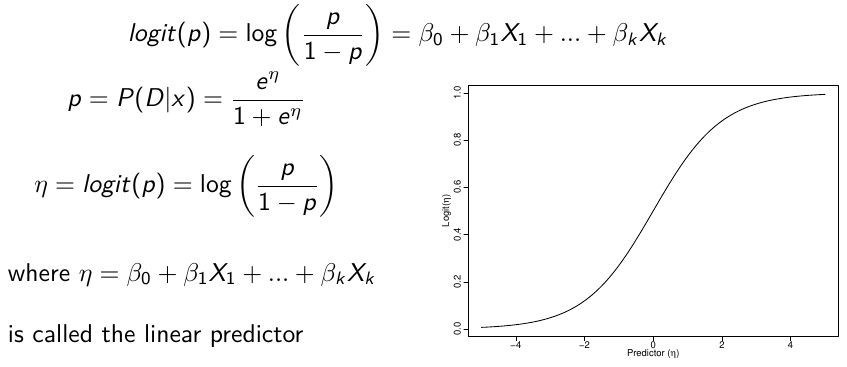
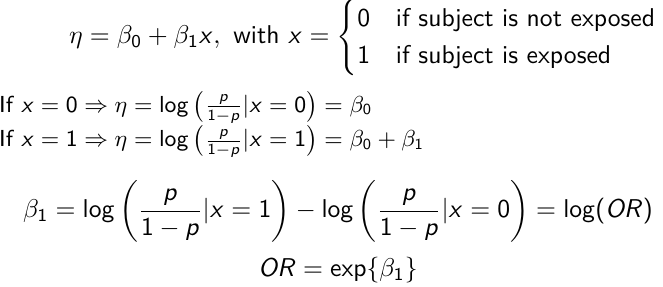
image.png

image.png
In a case-control study beta_0 is not interpretable. But the estimate of log(OR) can be interpreted correctly, given the symmetry of roles of disease/exposure

H0: OR = 1; Log(OR) = 0; No association
H1: OR != 1; Log(OR) != 0; Significant association

The Frequentist approach would be to simply fit a logistic regression in R using the function glm()

In Bayesian formulation we need to identify the parameters in our prior model, and the parameters we wish to estimate.

Ex. Below we model 2 parameters, beta_0 and beta_1, in a DAG model: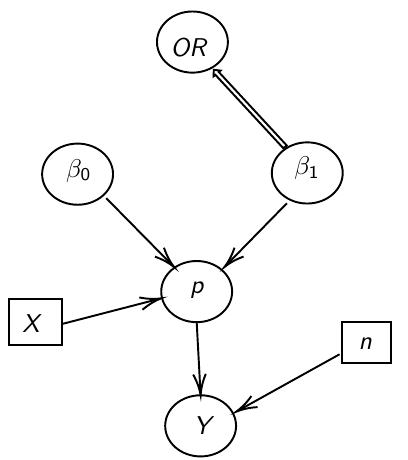
image.png

Because there's no constraint on the beta regression parameters, it is common to assume a normal distribution.
The magnitude of variance reflects the amount of uncertainty

In the below code:

  • We loop to specify each observation
  • Y.D[i] =
    • 1 if subject i has the disease
    • 0 if subject i does not have the disease
  • X.E[i] =
    • 1 if subject i has been exposed
    • 0 if subject i has not been exposed
# Analysis with JAGS
library(rjags)

model.1 <- "model{
### data model
for(i in 1:N){
    Y.D[i] ~ dbin(p[i], 1)
    logit(p[i]) <- beta_0 + beta_1*X.E[i]
}
OR <- exp(beta_1)
pos.prob <- step(beta_1)
### prior
beta_1 ~ dnorm(0,0.0001)
beta_0 ~ dnorm(0,0.0001)
 0 i th subject unexposed
}"
# In R Data stored as a list
data.1 <- list(N = 331, X.E = X.E, Y.D = Y.D)
# Compile model (data is part of it!); `adapt` for 2,000 samples
model_odds <- jags.model(textConnection(model.1), data = data.1,
n.adapt = 2000)
update(model_odds, n.iter = 5000) # 5,000 burn-in samples
# Get 10,000 samples from the posterior distribution of OR, beta_0,beta_1
test_odds <- coda.samples(model_odds, c("OR", "beta_1", "beta_0"), n.iter = 10000)
plot(test_odds)
summary(test_odds)

In the output, we'll often look for the point estimate to be the posterior mean. However, when posterior density is skewed, posterior median is sometimes preferable.

Back to top