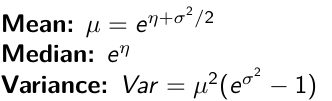Skip to main content

Bayesian Linear Regression

By now we know what a linear regression looks like. Let's consider a special case where number of parameters, p = 0: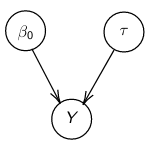
image.png
Assume Y is distributed as a normal distribution with mean β0:
Y|β0, τ ∼ N(β0, σ2 = 1/τ )

τ = 1 / σ2 , also called precision   <- Be aware this will be used interchangeably with variance

The density function is: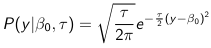
image.png
Mean and variance:
E(Y) = μ0; V(Y) = 1/τ0 + τ

The Posterior Distribution for β0 is calculated using Bayes' Theorem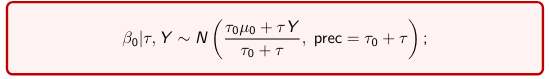image.png

When Mean and Variance are Unknown

We use a Normal prior distribution for the mean β0 ∼ N(μ0, τ0) and a Gamma prior distribution for the precision parameter: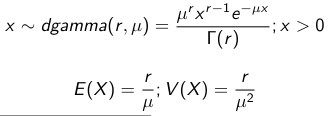
image.png

JAGS example:

model.1 <- "model {
	for (i in 1:N) {
		hbf[i] ~ dnorm(b.0,tau.t)
	}
	## prior on precision parameters
	tau.t ~ dgamma(1,1);
	### prior on mean given precision
	mu.0 <- 5
	tau.0 <- 0.44
	b.0 ~ dnorm(mu.0, tau.0);
    
    ### prediction
	hbf.new ~ dnorm(b.0,tau.t)
	pred <- step(hbf.new-20) # hbf >= 20
}"

Predictive Distributions

Given the Prior and Observed data we can compute the probability of a new observation will be greater or less than some integer threshold. The predictive distribution is a distribution of unobserved y~, that is: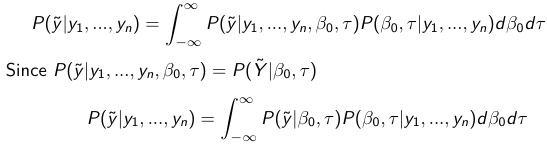
image.png

The two sources of variability in prediction are in the parameters V(β0, τ | y) and the variability in the new observation V(y | β0, τ)

  • To simulate from predictive density, do repeatedly:
    1. Sample one sample β0*, τ* from posterior β0, τ | y
    2. Sample one y~ ~ N(β0*, 1/τ* )
  •  During the Gibbs sampling we generate samples values from the posterior distribution β0, τ | y
  •  So Generating y~ ~ N(β0, τ | y) will produce the correct predictive distribution samples. P(y~ > 20 | data) is the proportion of y~ > 20

Log Normal Distributions

Since in the example above the outcome distribution can only be positive we can use a Log-Normal distribution, a continuous distribution with support for values y > 0.

image.png
Y | η, σ2 ~ INormal(η, σ2) with density function: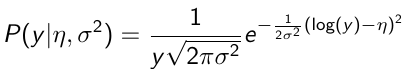
image.png

image.png

It also implies:     Log( Y )~ Normal(η, σ2)

In JAGS we use: dlnorm(η, σ2)

"model {
for (i in 1:N) {
	hbf[i] ~ dlnorm(lb.0,tau.t)
}

## prior on precision parameters
tau.t ~ dgamma(1,1);

### prior on mean
lb.0 ~ dnorm(1.6,1.6);

b.0 <- exp(lb.0)

### prediction
hbf.new ~ dlnorm(lb.0,tau.t)
pred <- step(hbf.new-20)
}"

In the above example, we get the initial prior on β0 from previous data, where we derived median(b.0)=5 and V(b.0)=1/0.44=2.27
Then we take the log of the median to get η and transform the precision variable with:  log(1 + V (b.0)/E (b.0)2 ), then take the inverse of that to get the variance.

 

Back to top