Bayesian Linear Regression

By now we know what a linear regression looks like. Let's consider a special case where number of parameters, p = 0: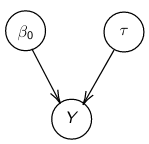

Assume Y is distributed as a normal distribution:
 Y|β₀, τ ∼ N(β₀, σ² = 1/τ )
The mean is β₀
τ = 1 / σ² , also called precision   <- Be aware this will be used interchangeably with variance
The density function is: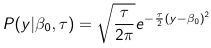

Mean and variance:
E(Y) = μ₀; V(Y) = 1/τ₀ + τ

The Posterior Distribution for β₀ is calculated using Bayes' Theorem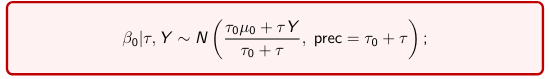

When Mean and Variance are Unknown

We use a Normal prior distribution for the mean β₀ ∼ N(μ₀, τ₀) and a Gamma prior distribution for the precision parameter: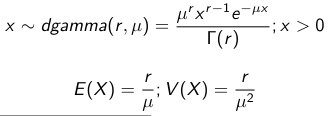

JAGS example:

model.1 <- "model {
	for (i in 1:N) {
		hbf[i] ~ dnorm(b.0,tau.t)
	}
	## prior on precision parameters
	tau.t ~ dgamma(1,1);
	### prior on mean given precision
	mu.0 <- 5
	tau.0 <- 0.44
	b.0 ~ dnorm(mu.0, tau.0);
}"

Predictive Distributions

Given the Prior and Observed data we can compute the probability of a new observation will be greater or less than some threshold. The predictive distribution is a distribution of unobserved y^~, that is: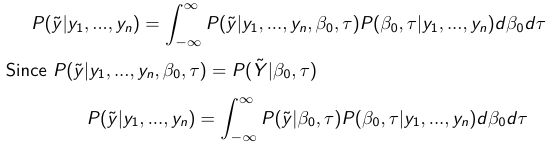

The two sources of variability in prediction are in the parameters V(β₀, τ | y) and the variability in the new observation V(y | β₀, τ)

• To simulate from predictive density, do repeatedly:
  1. Sample one sample β₀^*, τ* from posterior β₀, τ | y
  2. Sample one y^~ ~ N(β₀^*, 1/τ* )
•  During the Gibbs sampling we generate samples values from the posterior distribution β₀, τ | y
•  So Generating y^~ ~ N(β₀, τ | y) will produce the correct predictive distribution samples. P(y^~ > 20 | data) is the proportion of y^~ > 20