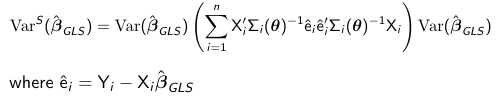Response Profile Analysis
Generalized Least Squares (GLS)
GLS is an extension of ordinary least squares (OLS) since it seeks to minimize a weighted sum of squared residuals. Unlike OLS, GLS accommodates heterogeneity and correlation via the weights which correspond to the inverse of the variance-covariance matrix. The parameters are estimated by minimizing the GLS objective function: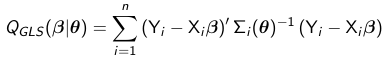
Theta is a vector of variance-covariance parameters. and 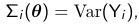
We distinguish 2 cases, where theta is known and theta is not known.
Theta is Known
From calculus we know that in order to minimize the objective function we
1. Differentiate with respect to beta
2. Set the result to 0
3. Solve for beta
The solution to the minimization of the problem is: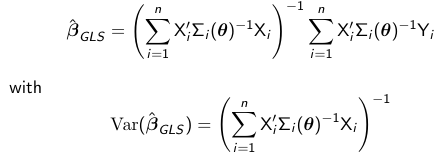
Since assuming we know the variance-covariance matrix of Y is a rather strong assumption we should protect ourselves against model mis-specification. We can use for inference the empirical "sandwich" estimator which is robust: