Multi-Level Modeling

MLM is designed to account for hierarchical or clustered structured data. Ex. patients by the same doctor, since patients with the same doctor might be more similar.

There are multiple ways to deal with hierarchical data. A simple approach is to aggregate, for example if 10 patients are sampled from each doctor we could take the average of all patients within a doctor rather than using individual patients' data. This would lead to consistent effect estimates and standard errors, but it does not really take advantage of all the data so we lose power.

Another approach is to analyze data from one high-level unit at a time, coming up with a regression model for every cluster. But again this does not make full use of the data.

The individual regressions have many estimates and lots of data but is noisy, and the aggregate method is less noisy but loses important differences by averaging all samples within each doctor. Linear mixed models (also called multi-level models) can be thought of as a trade off between these two alternatives.

Linear Mixed Models

The core of mixed models is that they incorporate fixed and random effects. While single  level models assume one variance, subjects within the same level are correlated in terms of σ0j2 + σ1j2Xij + εij

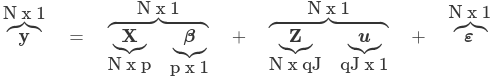
Where y is an N*1 column vector of the outcome
X is a N*p matrix of the p predictors
β is a p*1 matrix of the fixed effects regression coefficents
Z is the N*qJ design matrix for the random effects and J clusters and q random effects
u is a qJ*q vector of q random effects for J clusters/high-level units