Linear Mixed Effects Models

Here we'll be considering an alternative approach for analyzing longitudinal data using linear mixed effects models. These models have some subset of the individual parameters vary randomly from one subject to another, thereby accounting for sources of natural heterogeneity in the population.

• Fixed effects are the population characteristics that are assumed to be shared by all subjects
• Random effects are characteristics, unique for each subject
• The combination of both gives rise to mixed effect models

Model Formulation

The simplest mixed effects model for longitudinal data is:

Where b and e are independent.

The marginal mean response in the population is: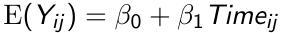

The response for the i^th subject at the j^th measurement occasion differs from the population mean response by a subject effect b_i, and a within subject measurement error e_ij.

The conditional mean response for any individual:

The residuals of profile analysis and parametric curves (ϵ_ij) and parametric curves such that ϵ_ij = b_i + e_ij

Variance and Covariance Structure

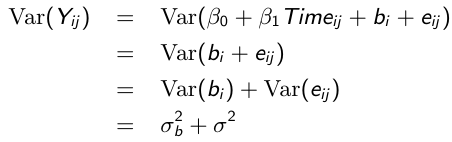
Similarly, the marginal covariance between any pair of responses: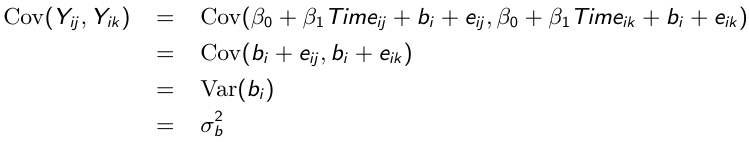

With some linear algebra we can write the variance-covariance matrix as follows: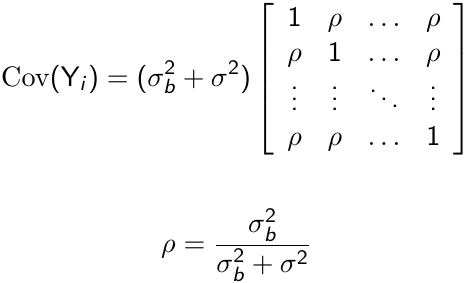

Where ρ is called the intra-cluster correlation coefficient. For ρ > 0, the random intercept mixed effects model is observationally equivalent to a compound symmetry model.

Random Intercept and Slope Model