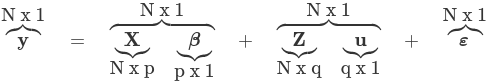Generalized Linear Mixed Effects Models
Generalized Linear Mixed Models (GLMMs) are an extension of linear mixed models to allow response variables from different distributions (such as binary or multi-nomial responses). Think of it as an extension of generalized linear models (e.g. logistic regression) to include both fixed and random effects.
- The general form of the model is: yij = Xij β + Zij bi + ε
- y (or sometimes η) is a N*1 column vector of the dependent (outcome) variable
- X is a N*p of the p predictor variables
- Z is the N*q design matrix for q random effects (the random complement to the fixed X)
- b (or sometimes u) is a q*1 vector of the random effects
- ε is an N*1 column of vector of the residuals (the part not explained by Xβ + Zu)
- y (or sometimes η) is a N*1 column vector of the dependent (outcome) variable
In classical statistics we do not actually estimate the vector of random effects; we nearly always assume that for the jth element of vector uj ~ N(0, G); Where G is the variance-covariance matrix of the random effects. Recall that the variance-covariance is always square, symmetric and positive semi-definite; This means for a q*q matrix there are q(q+1)/2 unique elements.
Because we directly estimated the fixed effects the random effect complements (Z) are modeled as deviations from the fixed effects with mean 0. The random effects are just deviations around the value in β (which is the mean). The only thing left to estimate is the variance. In a model with only a random intercept G is a 1*1 matrix (the variance of the random intercept). If we had a random intercept and a slope G would look like: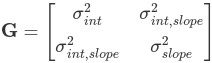
LMM VS GLMM
So far everything we've covered applied to both linear mixed models and generalized linear mixed models. What's different about these is that in GLMM the response variables can come from different distributions besides Gaussian. Additionally, rather than modeling the responses directly some link function (referred toi as g(.)) is often applied, such as log link.