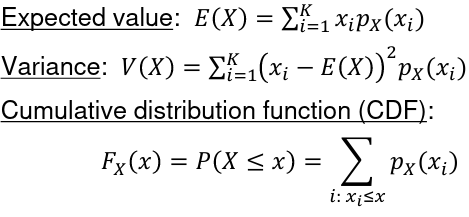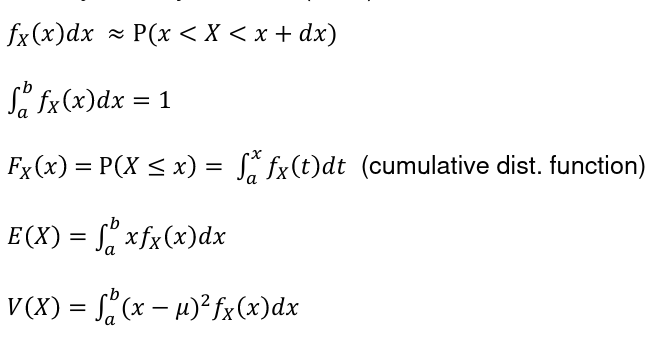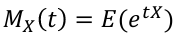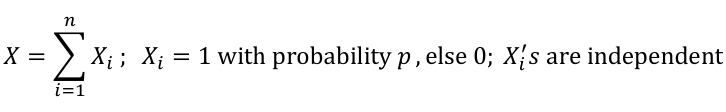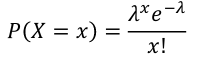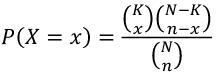Module 5: Multivariate Normal Distribution

A variable X follows a discrete probability distribution if the possible values of X are either:

• A finite set
• A countable infinite sequence

p_x(x_i) = P(X=x_i) is called the probability mass function (PMF)

• p_x(x_i)  >= 0 as it is a probability
  
• The sum of PMF for all values of X = 1

Recall that in a Discrete Probability Distribution :

In a Continuous Probability Distribution:

Moment Generating Function

Moments, such as E(X), V(X), can also be calculated using the Moment Generating Function (MGF):

The rth moment of X, E(X^r) can be obtained by differentiating M_x(t) r times with respect to t and setting t=0

• M_x(0) = 1
• M^I_x(0) = E(X)
• M^II_x(0) = E(X²) -> V(X) = M^II_x(0) - (MI_x(0))2
• In general, M_x^(r)(0) = E(X^r)

Uniqueness: if X and Y are two random variables and M_x(t) = M_y(t) when |t| < h for some positive number h, then X and Y have the same distribution

Note: MGF does not exist for all distributions (E(e^tx) may be infinity)

Binomial Distribution

X ~ Binomial(n, p)      𝑝 ∈ [0, 1]

X = the number of successes in n trials when the probability of success in each trail is p.

We can think of X as the sum of n independent Bernoulli(p) random variables, with the same p for every X_i

• PMF = P(X = x) = 
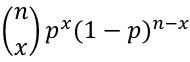
• Expected value = E(X) = np
• Variance = V(X) = np(1-p)
• MGF = M_x(t) = (pe^t + (1-p))ⁿ
• Two discrete random variables are independent if: P(X = x & Y = y) = P(X = x)*P(Y=y)

Poisson Distribution

X ~ Poisson(λ)     λ > 0

X = The number of occurrences of an event of interest.

• PMF = 
• Expected Values = E(X) = λ
• Variance = V(X) = λ
• MGF = M_x(t) = e^{λ(e^t - 1)}

Poisson as an approximation  of the Binomial Distribution

• If X ~ Binomial(n, p) and n -> infinity, p-> 0 such that np is a constant  =>  X ~ Poisson(np)
• Often used analyzing rare diseases

Geometric Distribution

X ~ Geometric(p)      𝑝 ∈ (0, 1]

If Y₁, Y₂, Y₃ ... are a sequence of independent Bernoulli(p) random variables then the number of failures before the first success, X, follows a Geometric distribution.

• PMF = P(X = x) = p(1-p)^x
• Expected value = E(X) = (1-p)/p
• Variance = V(X) = (1-p)/p²
• MGF = M_x(t) = p / (1 - (1 - p)e^t)

Hyper-Geometric Distribution

X ~ Hypergeometric(N, K, n)

Suppose a finite population of size N contains two mutually exclusive events: K success events and N-K failure events. If n events are randomly chosen without replacement X is the number of success events chosen.

• PMF = P(X = x) =
• Expected value = E(X) = nk / N
• Variance = V(X) = ((nK) / N) * ((N-K) / N) * ((N - n) / (N - 1))