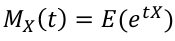Module 5: Multivariate Normal Distribution
A variable X follows a discrete probability distribution if the possible values of X are either:
- A finite set
- A countable infinite sequence
px(xi) = P(X=xi) is called the probability mass function (PMF)
- px(xi) >= 0 as it is a probability
- The sum of PMF for all values of X = 1
Moment Generating Function
Moments, such as E(X), V(X), can also be calculated using the Moment Generating Function (MGF):
The rth moment of X, E(Xr) can be obtained by differentiating Mx(t) r times with respect to t and setting t=0
- Mx(0) = 1
- MIx(0) = E(X)
- MIIx(0) = E(X2) -> V(X) = MIIx(0) - (MIx(0))2
- In general, Mx(r)(0) = E(Xr)
Uniqueness: if X and Y are two random variables and Mx(t) = My(t) when |t| < h for some positive number h, then X and Y have the same distribution
Note: MGF does not exist for all distributions (E(etx) may be infinity)