Module 14: Topics in Linear Regression

Assumption in Linear Regression:

• Independence between observations
  
• NormallyLinearity distributedbetween X and Y for any fixed value of X
• Homoscedasticity - the variance of Y is the same for any value of X
• LinearityNormally between X anddistributed Y (obviously)for any fixed value of X
  

Also, the model is also only generalizable to the population within the range of observed values of X.

Independence

The way we collect data or which data we collect determines independence. Examples of violated independence:

• Data comes from individuals that are related closely
• Multiple observations were collected over time for the same subject

Linearity

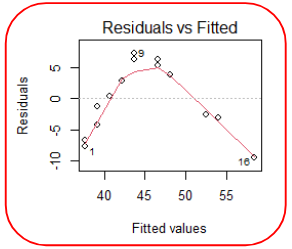
In order to test linearity, we would expect a graph of the residuals to be randomly scattered around the horizontal line. If there is a pattern to the residuals, the trend cannot be assumed to be linear.

The above residual plot shows a clear trend, thus the linear assumption is voilated.

Homoscedasticity

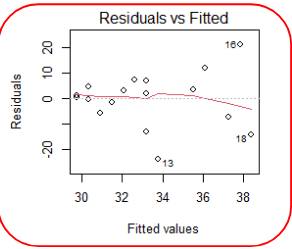
When talking about homoscedasticity, we require variance of error terms to be similar across independent variables. To assess homoscedasticity we can look at a scatterplot of y vs. x to determine if the spread in y is the same for each value of x.

Here we observe the spread of Y increasing as X increasing, thus the homoscedasticity assumption is not met.

Normality

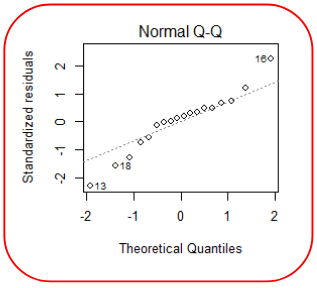
Finally for the normality of data we can examining the histogram of residuals and the QQ plot of residuals. If the data is normally distributed, the points will lie on the line.

Above is a example were the QQ of the residuals indicates a violation of normality.