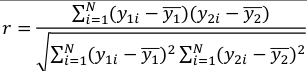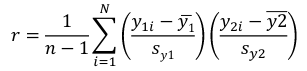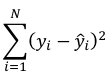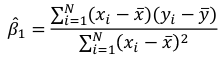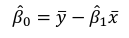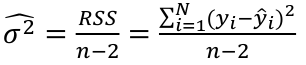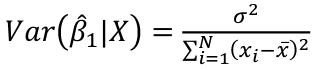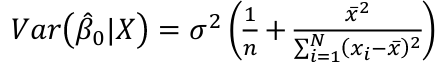Module 13: Linear Regression
Correlation and regression attempt to describe the strength and direction of the association between two (or more) continuous variables.
Pearson Correlation
Recall r is an estimate of population correlation coefficient:
It is always between -1 and 1. With 0 indicating no positive or negative linear relationship between the variables.
A strong correlation does not imply causality.
It indicates the strength and direction of a linear relationship between two random variables. The square of r, r2 = R, measures how much information is shared between two variables; It is also called the coefficient of determination.
r can also be expressed as the average product in standard units in terms of sample standard deviations:
Assumptions for Pearson's Correlation:
- Observations are independent
- The association is linear
- Variables are approximately normally distributed
We can compute a test statistic for r with a t-distribution:
t = r / se(r); Where SE of r = sqrt((1-r^2)/(n-2))
Note that se is inversely related to n, so a large sample size results in a smaller se(r). Also the test has n-2 degrees of freedom.
Simple Linear Regression
Linear regression is used to quantify the relationship between one or more independent variables (X) and a single dependent variables (Y). Simple linear regression is the case when we have 1 independent continuous variable and 1 dependent continuous variable.
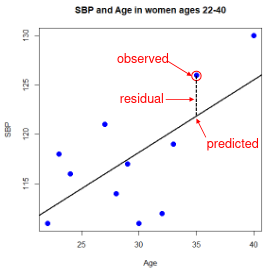
The line of best fit is the line which minimized the least squares (LS) estimate:
The sum of predicted minus observed values squared. For regressions with only one independent variable, X, this yields to the following equation:
Which simplifies to:
Even after we find our best fit line, we cannot predict values that were outside of our sample range.
Estimated Variances of Estimates
The square root of estimated variance is Standard Error (SE).
In R, the lm() function can be used to determine the simple linear regression:
res <- lm(var_y ~ var_x, data=mydata)
summary(res)