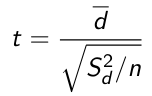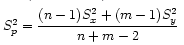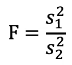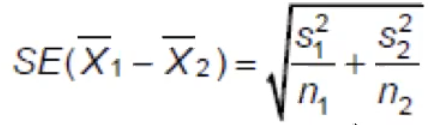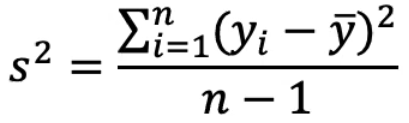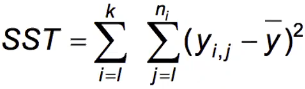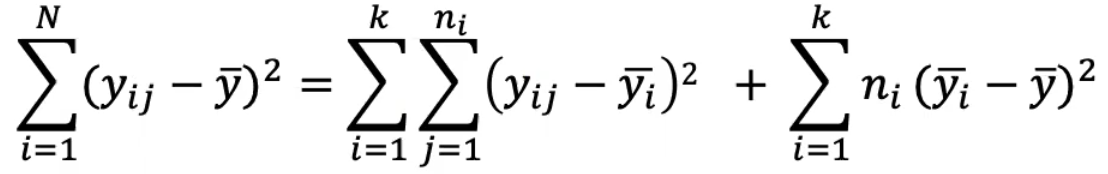Module 11: ANOVA - Analysis of Variance
ANOVA can be used to compare the means of several populations with continuous populations simultaneously. The population variance of the dependent variable must be equal in all groups.
Recall that
Which is the difference in two means over the standard error. When comparing multiple independent samples it is easier to use a pooled variance, but to do so the variances must be equal.
Equality of Variances
The equation for pool variance:
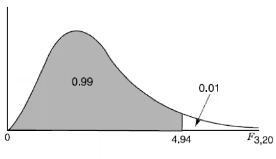
Assumption for pooled variance is that variances in the two groups are equal. We can test this with H0 = σ1=σ2 and use the F distribution which is indexed by the denominator df and the numerator df; choose the larger estimated variance to be numerator and the smaller estimated variance to be the denominator.
Test statistic:
If F is greater or smaller than critical values for a given significance level the null hypothesis is rejected and we can conclude there is evidence the two population variances are not equal.
The F distribution is not symmetric, which makes it hard to look up critical values. It can be done in R: pf(F, df1, df2, lower=F)
The F test is not always appropriate as it is sensitive to departures from normality. Examine variability in the two groups by comparing sample variances using boxplots to help decide which standard error is appropriate. In the case where variances are unequal we use the same procedure but SE is estimated as:
Using the n-1 degrees of freedom from whichever sample is smaller as an approximate (SAS or R would figure out the exact value).
ANOVA
Terminology:
- Factor - category/grouping variable
- Level - individual group of the factor
- Balanced design - same number of individuals in each level
The general data configuration is we have k population groups each with nk observations, which can be the same or different.
Assumptions:
- Observations are independent
- Data are random samples from k independent populations
- Within each population the dependent variable is normally distributed
- The population variance of the dependent variable is equal in all groups.
H0: The k populations means are equal
Ha : The k populations means are not all equal or at least one is not equal
Recall that variance as a function of Y is:
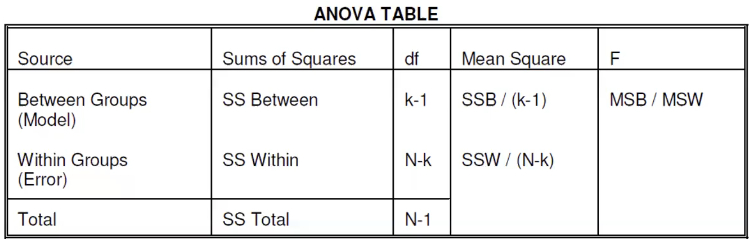
The numerator is the "Total variability" or the "Total sum of squares" (SST)
In ANOVA we split the SST into two components:
- Variability due to differences between the groups (SS Between Groups)
- Variability due to differences between individual y values within the groups (SS Within Group)
Which can also be expressed as:
SS Total = SS Within Groups + SS Between Groups
R2 is the proportion of variability explained by the difference between groups:
R2 = SS Between / SS Total
Adjustment Procedures
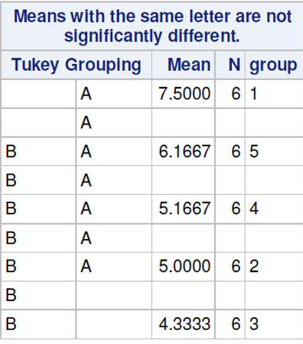
- Tukey's adjustment is appropriate when comparing pairs of means and is among the most powerful
- Provides exact P-values when groups are equal sizes
In the above Turkey procedure we observe group 1 and 3 are significantly different
- Scheffe's adjustment is appropriate for general contrasts
- Bonferroni's adjustment is appropriate for any situation but can be too conservative
Parametric vs Non-parametric Tests
Tests are parametric because they make assumptions about the distribution of the data.
Non-parametric methods make fewer and more generic assumptions about the distribution of the data. These tests are generally more friendly toward non-normal distributions and small sample sizes.
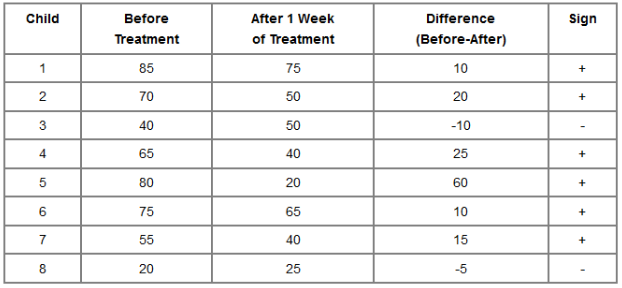
Sign Test
Simplest non-parametric test. Analyze only the signs of the differences:
H0: The median difference is zero (half the signs are positive and half are negative)
Ha: The median difference is not zero
Wilcoxon Signed-Rank Test
Paired-sample t-test equivalent. Uses information on the relative magnitude of the paired differences as well as their signs.
Assumption:
- Independent observations
- Continuous or ordinal observations
- Symmetric distribution
1. Rank the magnitude of the differences (ignoring the signs)
2. Attach the signs to the ranks to form signed ranks
3. Calculate the test statistic, R, which is the sum of the positive ranks.
4. n≥20 → normal approximation
The values of the test statistic will range from 0 to N(N+1)/2, with a mean value of N(N+1)/4