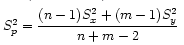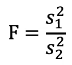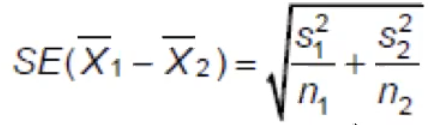Module 11: ANOVA - Analysis of Variance

ANOVA can be used to compare the means of several populations with continuous populations.

Equality of Variances

The equation for pool variance:

Assumption for pooled variance is that variances in the two groups are equal. We can test this with H0 = σ₁=σ₂ and use the F distribution which is indexed by the denominator df and the numerator df; choose the larger estimated variance to be numerator and the smaller estimated variance to be the denominator.

Test statistic:

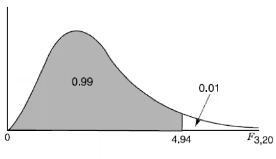
If F is greater or smaller than critical values for a given significance level the null hypothesis is rejected and we can conclude there is evidence the two population variances are not equal.

The F distribution is not symmetric, which makes it hard to look up critical values. It can be done in R: pf(F, df1, df2, lower=F)

The F test is not always appropriate as it is sensitive to departures from normality. Examine variability in the two groups by comparing sample variances using boxplots to help decide which standard error is appropriate. In the case where variances are unequal we use the same procedure but SE is estimated as:

Using the n-1 degrees of freedom from whichever sample is smaller as an approximate (SAS or R would figure out the exact value).