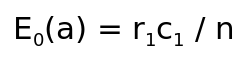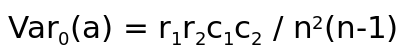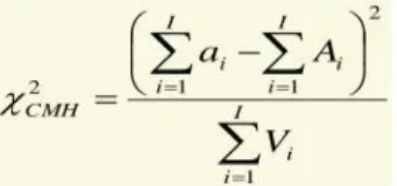Module 10: Confounding and MH Method
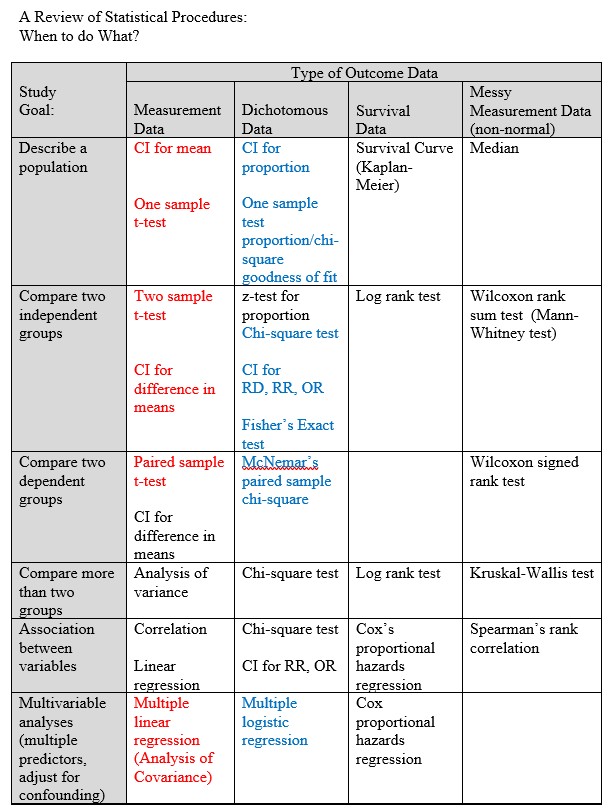
With categorical data, we are classifying data instead of measuring it. As a review:
Notice we never use a z test, a t test is almost always more appropriate even for large samples. Likewise, for dichotomous outcomes could use a z-test but a chi-square test is usually used in practice. Chi-square reflects categorical outcomes.
chi-square = sum((obs-exp)2 / exp), df=n-1; where n is the number of random variables or categories.
Mantel-Hansel Method
Cochran-Mantel-Haenszel method is a technique that generates an estimate of an association between an exposure and an outcome after adjusting for or taking into account confounding. We stratify the data into two or more levels of the confounding factor (as we did in the example above). In essence, we create a series of two-by-two tables showing the association between the risk factor and outcome at two or more levels of the confounding factor, and we then compute a weighted average of the risk ratios or odds ratios across the strata.
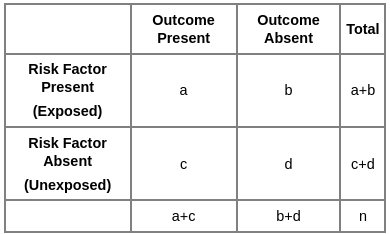
Given the above table, we have the below MH Equations:
For Cell(1,1) frequency has
and
For each table, and the MH test statistic is:
It follows a Chi-Square distribution with 1 degree of freedom.
We can also derive the following:
Though, in practice we just have the computer solve for MH estimates.