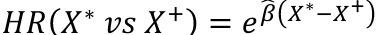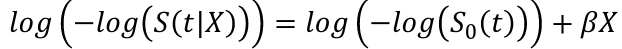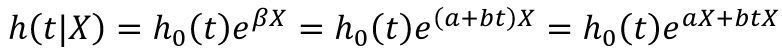Skip to main content

Survival Analysis II

In survival data the dependent variable is always survival time (or time until an event with the potential to censor observations). The independent variable can be any type; Continuous, ordinal or categorical. We assume the observations are independently and randomly drawn from the population.

Kaplan-Meier estimator allows crude comparison between two groups, but it does not provide an effect estimate or allow adjustment for covariates.

Cox Proportional Hazards Model

In 1972 Sir David Cox introduced a survival model in which the hazard function changes with time only through the baseline function.

We can model the hazard as a function of the exposure and quantify the relative hazard, which allows for adjustment of covariates. This is the instantaneous failure rate, or the event rate over a small interval or time. The hazard ratio does not depend on time. The hazard baseline function is modeled as: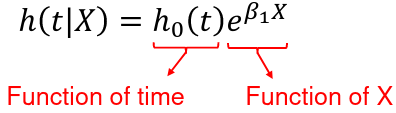
image-1667834824976.png
A hazard ratio at time t for a change in X: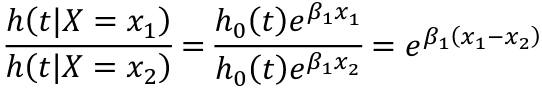
image-1667835012915.png

The baseline hazard function, h0(t) when X=0, is treated as a nuisance function and is left unspecified (non-parametric part of the model). The covariates affect the hazard function multiplicatively through the function exp(Beta*X) (the parametric part of the model).

image-1667835582244.png

The model is therefore called a semi-parametric model. It is suitable when we are more interested in the parameter estimates (effects of covariates) than the shape of the hazard. Fit by maximizing the partial likelihood.

X = 0
image-1667835492684.png
X = 1
image-1667835515079.png
Hazard ratio X=1 vs X=0
image-1667835549920.png

image-1667835628151.png
CI is similar to logistic regression, we only model the hazard rather than the odds. Situations in which you might expect the logistic and PH regression results to differ:

  • Common event (cumulative risk for the event is not small)
  • Differential loss to follow-up (loss differs by exposure)
  • Exposures change over follow-up

Tied Event Times

  • Breslow's Method
    • An approximation to the exact adjustment
    • Default option in SAS
  • Efron's method
    • A different approximation to the exact adjustment
    • A better approximation than Breslow's method
    • Default in R / SAS: "ties=efron" in PROC PHREG
  • Kalbfleisch and Prentice's "exact" method
    • Assumes ties are due to imprecise measurement of time
    • Most computationally-intensive method (all possible ordering of tied data is considered)
    • Not available in R / SAS: "ties=exact" in PROC PHREG

All will give the identical estimates if there are no ties.

Proportional Hazards Assumption

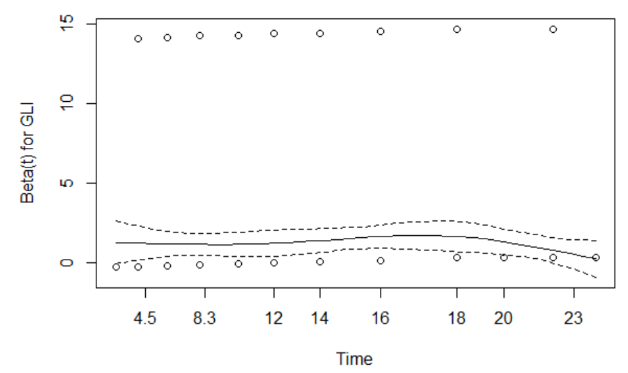
Beta should not change with time if the proportional hazards assumption holds.

H0: Proportional hazard is satisfied
Conclusion: We fail to reject the null hypothesis, so no evidence of departure from the PH assumption

  • Graphical Method: log(-log(S(t))) plot
    • The natural logs of h(t | X) plotted against time are parallel for varying values of X, separated by Beta
    • Likewise, the log of the negative log of S(t | X) plotted against time (or log(time)) are parallel for varying values of X, separated by Beta

      image-1667838767138.png

  • Schoenfeld Residuals
    • Suppose subject i has an event at time tt
    • The Schoenfeld residual for subject i and covariate X is: 
      • xi - x_bar(ti), where x_bar(ti) is the estimated mean of X based on the subjects at risk at time ti (similar to observed - expected)
    • A test of the PH assumption is based on a test of the correlation between sccaled Schoenfeld residuals and a function of time
      • If the PH assumption is satisifed the Schoenfeld residuals should be uncorrelated with time
      • A significant test (small p-value) suggests that the PH assumption fails
    • If the proportional hazards assumption is satisfied the plot should look like a horizontal line
    • In R: 'cox.zph(linreg)'

      image-1667839458586.png

  • Time-varying Effects
    • SAS and R have internal algorithms to build the "time-varying covariates", this is NOT the same as including a time covariate interaction in the model.
    • In this method we think of Beta as a function of time:
      Beta = a + bt

      image-1667839687887.png

  • Martingale Residuals (SAS Only)
    • Using ASSESS statement in SAS
    • Assess both functional form and proportional hazards assumption for each covariate using simulation
    • A set value needs to be set to reproduce results
    • The observed path (solid line) should not be extreme compared to the simulated paths (dashed lines)
Which Test to Use?

A method should be choosen ahead of time. Tests based on Schoenfeld residuals and time-varying effects are the most commonly reported.

R Code

library(survival)
framdat4 <- read.csv("framdat4.csv", header=T, na.strings=c("."))

## Cox Proportional Hazards regression
### Crude Model    

# Fit the model: coxph()
fit.1 <- coxph(Surv(chdtime, chd_sw) ~ GLI, data=framdat4)
summary(fit.1)


### Adjusted Model
fit.2 <- coxph(Surv(chdtime, chd_sw) ~ GLI+AGE+SPF+CSM+FVC+MRW, data=framdat4)
summary(fit.2)

## Assess the PH assumption
### Log(-Log(Survival)) Plot
fit.km <- survfit(Surv(chdtime, chd_sw) ~ GLI, data=framdat4)

# Method 1: use the fun="cloglog" option
plot(fit.km, col=c("black", "red"), fun="cloglog",  main="Log of Negative Log of Estimated Survival", 
     xlab="time", ylab="log(-log(survival))", cex.main=1.5, cex.axis=1.5, cex.lab=1.5)
legend(x=12, y=-3.5, legend=c("No GLI","GLI"), col=c(1,2), lwd=1, cex=1.2)

# Method 2: calculate the logs manually
plot(log(fit.km$time),log(-log(fit.km$surv)), main="Log of Negative Log of Estimated Survival", 
     xlab="log(time)", ylab="log(-log(survival))", cex.main=1.5, cex.axis=1.5, cex.lab=1.5)
lines(log(fit.km$time[1:12]), log(-log(fit.km$surv[1:12])), lwd=2)
lines(log(fit.km$time[13:24]), log(-log(fit.km$surv[13:24])), lwd=2, col=2)
legend(x=2.5, y=-3.5, legend=c("No GLI","GLI"), col=c(1,2), lwd=2, cex=1.2)

### Schoenfeld residuals
# Assess the PH assumption: cox.zph()
test.1 <- cox.zph(fit.1)
print(test.1)
plot(test.1)

test.2 <- cox.zph(fit.2)
print(test.2)
plot(test.2)

### Time-Varying Covariates to assess PH assumption
# Use the 'tt' option
# (1) Interaction with time
fit.a <- coxph(Surv(chdtime, chd_sw) ~ GLI+tt(GLI), data=framdat4, 
                   tt=function(x,t,...)x*t)
summary(fit.a)
# plot HR
plot(c(0:25), exp(1.46-0.024*c(0:25)), type="l", xlab="Time (years)", ylab="HR", col="blue", lwd=2)

# (2) Interaction with log(time)
fit.b <- coxph(Surv(chdtime, chd_sw) ~ GLI+tt(GLI), data=framdat4, 
                   tt=function(x,t,...)x*log(t))

summary(fit.b)
# plot HR
plot(c(0:25), exp(1.28-0.05*log(c(0:25))), type="l", xlab="Time (years)", ylab="HR", col="blue", lwd=2)
 
### Stratified analysis
# Create age strata
age.group <- rep(1, nrow(framdat4))
age.group[ which(framdat4$AGE >44 & framdat4$AGE <55)] <-2
age.group[ which(framdat4$AGE >54 & framdat4$AGE <65)] <-3
age.group[ which(framdat4$AGE >64 & framdat4$AGE <75)] <-4

# Fit stratified model using strata() option
fit.s <- coxph(Surv(chdtime, chd_sw) ~ GLI+SPF+CSM+FVC+MRW+AGE+strata(age.group),
               data=framdat4)
summary(fit.s)

cox.zph(fit.s)
Back to top