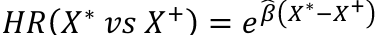Survival Analysis II
In survival data the dependent variable is always survival time (or time until an event with the potential to censor observations). The independent variable can be any type; Continuous, ordinal or categorical. We assume the observations are independently and randomly drawn from the population.
Kaplan-Meier estimator allows crude comparison between two groups, but it does not provide an effect estimate or allow adjustment for covariates.
We can model the hazard as a function of the exposure and quantify the relative hazard, which allows for adjustment of covariates. This is the instantaneous failure rate, or the event rate over a small interval or time. The hazard ratio does not depend on time. The hazard baseline function is modeled as: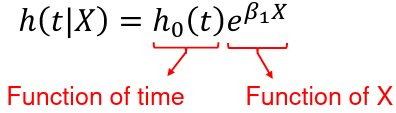
A hazard ratio at time t for a change in X: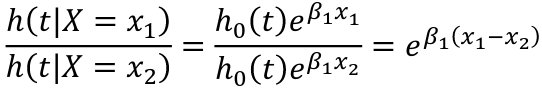
Cox Proportional Hazards Model
In 1972 Sir David Cox introduced a survival model in which the hazard function changes with time only through the baseline function.
The baseline hazard function, h0(t) when X=0, is treated as a nuisance function and is left unspecified (non-parametric part of the model). The covariates affect the hazard function multiplicatively through the function exp(Beta*X) (the parametric part of the model).
The model is therefore called a semi-parametric model. It is suitable when we are more interested in the parameter estimates (effects of covariates) than the shape of the hazard. Fit by maximizing the partial likelihood.
X = 0![]()
X = 1![]()
Hazard ratio X=1 vs X=0![]()