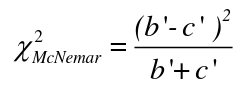Skip to main content

Matching

The aim of matching is remove confounding by matching subjects to be similar on a potential confounder. Doing so eliminates (or reduces) confounding, as well as reducing variability thereby increasing power.

Recall a paired t-test with two independent samples: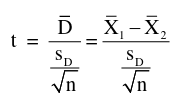
image-1664806890708.png
with n-1 degrees of freedom and standard error: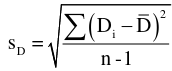
image-1664806918982.png
The test is inversely related to variance.

Types of Matching

  • Matched Pairs (covered today)
  • Categorical Matching (unmatched analysis, stratified or regression)
    • Stratify cases, then find equal number of controls for each category (or equal multiple).
  • Caliper Matching
    • Only for continuous variables
    • Similar to categorical but not the same
  • Nearest Neighbor
    • Select 'closest' control as match
    • May have minimum match criteria

Matching in Follow-Up Study

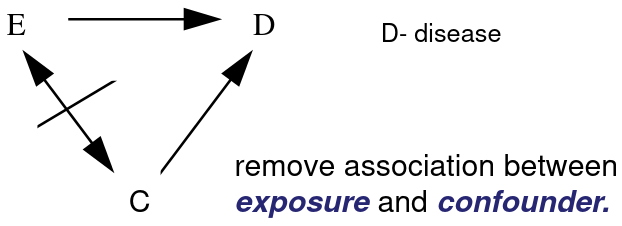
image-1664805506582.png
Remove Confounding (C) in the study sample between Exposed (E) and unexposed by matching on the potential confounders.

There are 4 possible combinations of outcomes in exposed and unexposed groups: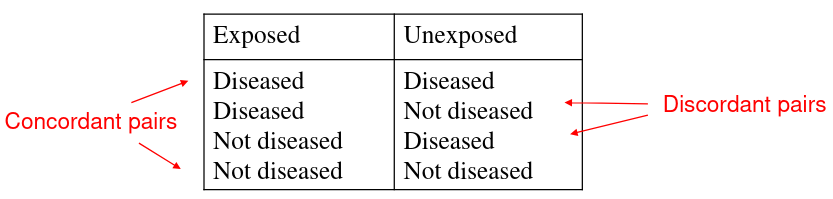
image-1664807476717.png
Corncordant pairs have the same outcome between pairs, and opposite in discordant pairs.

An example presentation for matching 2x2 tables: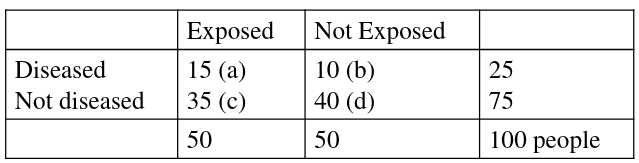
image-1664807990551.png
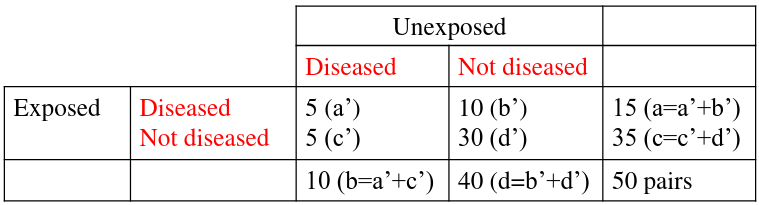
image-1664807969489.png
Notice the column and cell totals now equal the value of cells a,b,c,and d in the original table.

If we take the Risk Ratio of both the above tables, we find they are both the same (1.5).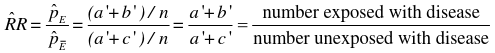
image-1664808244709.png

Matching in Case-Control Study

image-1664806210348.png
Remove Confounding (C) in the sample study between cases and controls by matching on potential confounders where for each case we select a control with the same values for the confounding variables.

For case control studies we set up our pairs differently:

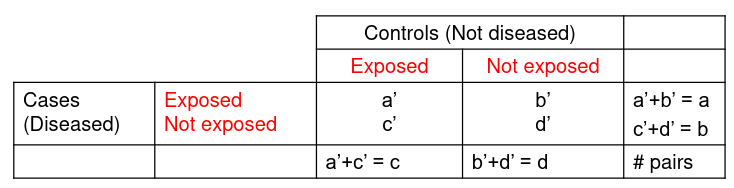
image-1664808714918.png
We can then express the odds ratio as: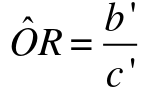
image-1664808739147.png

The McNemar Test

The McNemar Test is a non-parametric test for paired nominal data. It is a chi-square distribution and can be used for retrospective case-control or follow-up studies. It assumes:

  • The two groups are mutually exclusive
  • A random sample

H0: The proportion of some disease is the same in participants with exposure and those without exposure (RR=1)
Ha: The proportion of some disease is  not the same in participants with exposure and those without exposure (RR != 1)

image-1664808475923.png with df = 1

 

Back to top