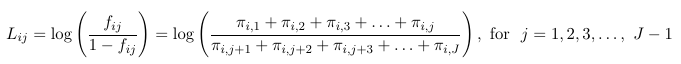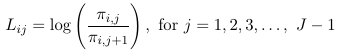GLM for Multinomial Outcomes
Multinomial outcomes are much akin to binomial outcomes, with added complexity due to outcomes with more than 2 levels. In such cases it can be difficult to determine an 'order' to the outcomes.
Log-linear models can be used for analysis of this type of data. For example, if we have some distribution where πij represents the probability that the ith individual falls under the jth category. Assuming the response categories are mutually exclusive: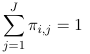
For each individual i; That is the probabilities add up to 1 for each individual, so we only have J - 1 probability parameters.
Multinomial Distribution
This is an extension of the binomial distribution involving joint distributions. Specifically each trial can result in any of the k events (E1, E2 ... Ek), each with its own respective probabilities. The probability that in n trials we observe Y1 of the E1 outcomes, y2 of the R2 outcomes ... and yk of the Rk outcomes in n independent trials is:![]()
with y1 + y1 .. + yk = n and the probabilities summing to 1
The multinomial term: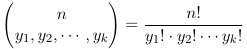
represents the number of possible divisions of n distinct objects into k distinct groups of sizes y1, y2... yk
Consider an example with k = 3 (three possible outcomes):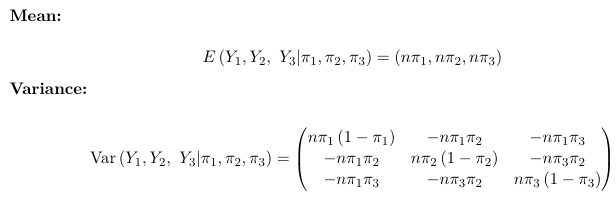
The multinomial distribution model counts are negatively correlated; The dispersion parameter is φ = 1
The binomial distribution can be thought of as a particular case of the multinomial distribution with k = 2. We want models for the mean of the response or equivalently for the probabilities, where the probabilities depend on a vector of covariates.
Link Function - Generalized Logits
Perhaps the simplest approach to the Multinomial regression is to designate one of the response categories as the reference category and calculate the log-odds for all other categories relative to the reference. For the binomial example, the reference cell is often the 'non-event' category.
So for a multinomial with J categories there are J - 1 distinct odds. For example, in a case with 3 response categories we could use the last category as the reference and hence get 2 generalized odds also called generalized logits: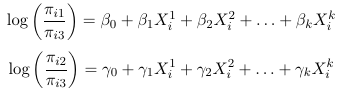
This is kind of like running 2 separate logistic regressions and estimating two separate sets of parameters, but it is a single model and all parameters are estimated by the MLE.
We can solve for the probabilities as a function of the slope parameters (beta and gamma):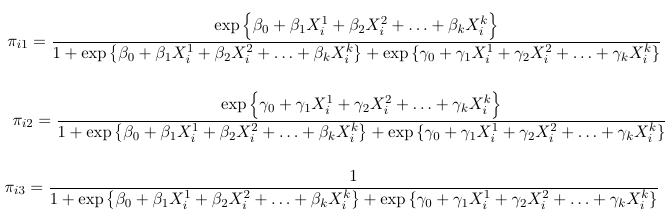
Thus, for a multinomial response with J categories, the J - 1 generalized logits are: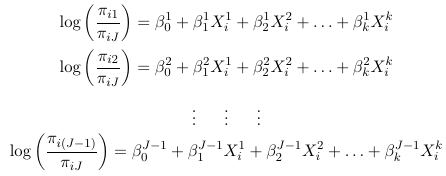
And then maximum likelihood can be used to estimate all parameters. For the intercept and each predictor, we will be estimating J - 1 parameters. Note that it really makes no difference which category is the reference, as we can always convert from one model formulation to another.
Interpretation
The generalized odds of having a response j relative to J are: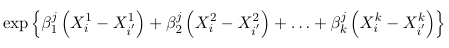
times higher for an individual with characteristics Xi1, Xi2, Xi3... Xik than for a individual with characteristics Xi'1, Xi'2, Xi'3... Xi'k. In particular, keeping X2 through Xk constant for each increase of one unit in X1 the odds of having a response j relative to J changes by a multiplicative factor of exp(beta1j)
Multinomial Ordinal Responses
Consider a multinomial random varaible Yi that may take one of J outcomes, assume there is a natural order from 1 to J. The probability falls into category j or lower is fij = P(Yi <= j), also called the cumulative probabilities.
When we have a clear order between categories several alternative regression models are available. We could use generalized logits model but it ignores the order of the levels and this have diminished power. The drawback of multinomial logits compared to general multinomial logits is that assumptions imposed may not be valid. We consider 3 types of models in which the order of the factors is relevant:
- Cumulative Logits models - most widely used
- Adjacent-Categories Logits models (next lecture)
- Continuation-Ratio Logits models (next lecture)
SAS Code
/* Contraceptive data 1=Sterilization,2=Other, 3=None*/
data contra;
input age method count ref total;
cage=age-4;
agesq=cage**2;
elsn=log((count/total)/(ref/total));
datalines;
1 1 3 232 296
1 2 61 232 296
1 3 232 232 296
2 1 80 400 617
2 2 137 400 617
2 3 400 400 617
3 1 216 301 648
3 2 131 301 648
3 3 301 301 648
4 1 268 203 547
4 2 76 203 547
4 3 203 203 547
5 1 197 188 435
5 2 50 188 435
5 3 188 188 435
6 1 150 164 338
6 2 24 164 338
6 3 164 164 338
7 1 91 183 284
7 2 10 183 284
7 3 183 183 284
;
run;
goptions reset=all ftext='arial' htext=1.2 hsize=9.5in vsize=7in aspect=1 horigin=1.5in vorigin=0.3in ;
goptions device=emf rotate=landscape gsfname=TempOut1 gsfmode=replace;
filename TempOut1 "C:\Projects\BS853\Class 7\contraceptive.emf";
axis1 label=('AGE') minor=none order=(1 to 7 by 1) value=(tick=1 '15-19' tick=2 '20-24' tick=3 '25-29' tick=4 '30-34' tick=5 '35-39'
tick=6 '40-44' tick=7 '45-49') ;
axis2 label=(a=90 'Log Generalized Logit (None as reference)') minor=none ;
symbol1 v=circle i=j cv=red ci=blue;
symbol2 v=dot i=j cv=green ci=magenta;
legend1 value=('Sterilization' 'Other') label=('Method') ;
proc gplot data=contra;
plot elsn*age=method/vaxis=axis2 haxis=axis1 legend=legend1;
where method in (1,2);
run;
/*Model 1*/
options ls=97 nodate pageno=1;
title1 'Contraceptive data';
title2 'Using PROC LOGISTIC - AGE categorical';
proc logistic data=contra order=data;
freq count;
class age method/param=glm;
model method=age/link=glogit;
contrast '1 vs 2' age 1 -1 0 0 0 0 0 /estimate=exp;
run;
/*Using Genmod*/
title2 'Using PROC GENMOD- AGE categorical';
proc genmod data=contra order=data;
class method age;
model count = method age method*age/dist=p;
run;
title2 'Using PROC CATMOD- AGE categorical';
proc catmod data=contra order=data;
weight count;
model method=age;
run;
/*Model 2 */
title2 'Using PROC LOGISTIC - continuous age linear effect';
proc logistic data=contra order=data;
freq count;
model method=cage/link=glogit;
run;
title2 'Using PROC CATMOD - continuous linear effect';
proc catmod data=contra order=data;
direct cage;
weight count;
model method=cage;
run;
/*Model 3*/
title2 'Using PROC LOGISTIC - continuous age linear and quadratic effects';
proc logistic data=contra order=data ;
freq count;
model method=cage agesq/link=glogit ;
output out=aa(where=(_level_ in (1,2) and method in (1,2) and method=_level_)) xbeta=pred;
run;
title2 'Using PROC CATMOD - continuous age linear and quadratic effects';
proc catmod data=contra order=data;
direct cage agesq;
weight count;
model method=cage agesq;
run;
/*Using Genmod*/
title2 'Using PROC GENMOD - continuous age linear and quadratic effects';
proc genmod data=contra;
class method age;
model count = method age method*cage method*agesq/dist=p;
run;
filename TempOut1 "C:\Projects\BS853\Class 7\contraceptivepred1.emf";
axis1 label=('AGE') minor=none order=(1 to 7 by 1) value=(tick=1 '15-19' tick=2 '20-24' tick=3 '25-29' tick=4 '30-34' tick=5 '35-39'
tick=6 '40-44' tick=7 '45-49') ;
axis2 label=(a=90 'Log Generalized Logit (None as reference)') minor=none ;
symbol1 v=circle i=j cv=red ci=blue;
symbol2 v=dot i=j cv=green ci=magenta;
legend1 value=('Observed' 'Predicted') label=('') ;
title1 h=1.2 'Predicted vs. Observed For Method=Sterilization';
proc gplot data=aa;
plot elsn*age pred*age/vaxis=axis2 haxis=axis1 overlay legend=legend1;;
where method=1;
run;
/* Using SGplot */
ods listing gpath="Z:/Documents/BS853/Spring 2019/Class 6/";
ods graphics / reset width=600px height=400px imagename="Pred1" imagefmt=gif;
title1 h=1.2 'Predicted vs. Observed For Method=Sterilization';
proc sgplot data=aa cycleattrs;
yaxis grid label="Log Generalized Logit (None as reference)";
xaxis grid label="Age";
series x=age y=elsn / lineattrs = (pattern=solid thickness=3)
legendlabel = "Observed Data" name= "elsn";
scatter x=age y=elsn/ markerattrs=(symbol=circlefilled size=10 color=orange);;
series x=age y=pred / lineattrs = (pattern=solid thickness=3)
legendlabel = "Model" name= "pred";
scatter x=age y=pred/ markerattrs=(symbol=squarefilled size=10 color=green);
keylegend "elsn" "pred";
where method=1;
run;
filename TempOut1 "C:\Documents and Settings\doros\My Documents\Projects\BS853\Class 7\contraceptivepred2.emf";
title1 h=1.2 'Predicted vs. Observed For Method=Other';
proc gplot data=aa;
plot elsn*age pred*age/vaxis=axis2 haxis=axis1 overlay legend=legend1;;
where method=2;
run;
/* Using SGplot */
ods listing gpath="Z:/";
ods graphics / reset width=600px height=400px imagename="Pred2" imagefmt=gif;
title1 h=1.2 'Predicted vs. Observed For Method=Other';
proc sgplot data=aa cycleattrs;
yaxis grid label="Log Generalized Logit (None as reference)";
xaxis grid label="Age";
series x=age y=elsn / lineattrs = (pattern=solid thickness=3)
legendlabel = "Observed Data" name= "elsn";
scatter x=age y=elsn/ markerattrs=(symbol=circlefilled size=10 color=orange);;
series x=age y=pred / lineattrs = (pattern=solid thickness=3)
legendlabel = "Model" name= "pred";
scatter x=age y=pred/ markerattrs=(symbol=squarefilled size=10 color=green);
keylegend "elsn" "pred";
where method=2;
run;
/*Schoolchildren learning style preference and School program*/
/* styles 1=Self,2=Team,3=Class*/
data school;
do style=1 to 3;
input school program $ count @@;
output;
end;
cards;
1 Regular 10 1 Regular 17 1 Regular 26
1 After 5 1 After 12 1 After 50
2 Regular 21 2 Regular 17 2 Regular 26
2 After 16 2 After 12 2 After 36
3 Regular 15 3 Regular 15 3 Regular 16
3 After 12 3 After 12 3 After 20
run;
title1 'Estimating parameters using contrast statement';
options ls=97 nodate pageno=1;
ods select contrastestimate;
proc logistic data=school order=data;
freq count;
class school program/param=glm;
model style=school program /link=glogit;
contrast 'reg vs. after' program -1 1/estimate=exp;
run;
/*Consider data on association of cumulative incidence of
pneumoconiosis and years working at a coalmine.*/
data ph;
do type=1 to 3;
input age count @@;
output;
end;
cards;
1 218 1 13 1 12
2 71 2 25 2 32
run;
options ls=97 nodate pageno=1;
title1 'Cumulative Logit models - PROC GENMOD';
proc genmod data=ph order=data descending;
freq count; /*<-group data*/
class age;
model type = age / dist=multinomial link=cumlogit type3;
estimate 'LogOR12' age -1 1 / exp;
run;
title1 'Cumulative Logit models - PROC LOGISTIC';
proc logistic data=ph order=data descending;
freq count;
class age/param=glm;
model type = age;
contrast 'LogOR12' age -1 1 / estimate=exp;
run;
/* Metal Impairement data - Agresti, 1990*/
proc import datafile="Z:\Documents\BS853\Spring 2015\Class 6\impair.xls"
out = mimpair replace;
run;
options ls=97 nodate pageno=1;
title1 'Cumulative Logit models - PROC GENMOD';
proc genmod data=mimpair rorder=data;
model level = SES EVENTS/ dist=multinomial link=cumlogit type3;
estimate 'LogOR12' SES 1 / exp;
run;
title1 'Cumulative Logit models - PROC LOGISTIC';
proc logistic data=mimpair order=data ;
class level;
model level = SES EVENTS ;
contrast 'LogOR12' SES 1 / estimate=exp;
run;
/*satisfaction with THR and hospital volume and year of surgery.*/
proc format ;
value vol 1='High' 0='Low';
run;
data thr;
input year highvol satisf count total123 total12;
if satisf=1 then cuml1=log(count/(total123-count));
if satisf=2 then cuml2=log(total12/(total123-total12));
format highvol vol.;
datalines;
1 0 1 84 414 315
1 0 2 231 414 315
1 0 3 99 414 315
1 1 1 473 1059 966
1 1 2 493 1059 966
1 1 3 93 1059 966
2 0 1 150 614 497
2 0 2 347 614 497
2 0 3 117 614 497
2 1 1 332 781 719
2 1 2 387 781 719
2 1 3 62 781 719
3 0 1 257 1380 1146
3 0 2 889 1380 1146
3 0 3 234 1380 1146
3 1 1 571 1476 1364
3 1 2 793 1476 1364
3 1 3 112 1476 1364
;
run;
/* Only main effects model */
options ls=97 nodate pageno=1;
title1 'Only main effects model';
proc logistic data=thr ;
freq count; /* <- to deal with the grouped data */
class year;
model satisf=highvol year/aggregate scale=n; /* Aggregate and scale=n to get goodness of fit stats*/
run;
/* Only volume main effect in the model */
options ls=97 nodate pageno=1;
title1 'Only volume effect model';
proc logistic data=thr ;
freq count;
class ;
model satisf=highvol/aggregate scale=n;
run;
/* Only volume main effect in the model */
options ls=97 nodate pageno=1;
title1 'Only volume effect model';
proc logistic data=thr ;
freq count;
class ;
model satisf=highvol;
output out=bb(where=(_level_ in (1,2) and satisf in (1,2) and satisf=_level_)) xbeta=pred;
run;
goptions reset=all ftext='arial' htext=1.2 hsize=9.5in vsize=7in aspect=1 horigin=1.5in vorigin=0.3in ;
goptions device=emf rotate=landscape gsfname=TempOut1 gsfmode=replace;
filename TempOut1 "C:\Documents and Settings\doros\My Documents\Projects\BS853\Class 7\contraceptive.emf";
filename TempOut1 "C:\Projects\BS853\Class 7\hr1.emf";
axis1 label=('Year') minor=none order=(1 to 3 by 1) value=(tick=1 '1994' tick=2 '1995' tick=3 '1996') ;
axis2 label=(a=90 'Log Cumulative Logit ') minor=none ;
symbol1 v=circle cv=red pointlabel=(h=1.2 "#highvol");
symbol2 v=dot cv=green pointlabel=(h=1.2 "#highvol");;
legend1 value=('Observed' 'Predicted') label=('') ;
title1 h=1.2 'Very vs. Somewhat or Not satisfied';
proc gplot data=bb;
plot cuml1*year pred*year/vaxis=axis2 haxis=axis1 overlay legend=legend1;;
where satisf=1;
run;
filename TempOut1 "C:\Documents and Settings\doros\My Documents\Projects\BS853\Class 7\hr2.emf";
title1 h=1.2 'Very or Somewhat vs. Not satisfied';
proc gplot data=bb;
plot cuml2*year pred*year/vaxis=axis2 haxis=axis1 overlay legend=legend1;;
where satisf=2;
run;