GLM for Multinomial Outcomes
Multinomial outcomes are much akin to binomial outcomes, with added complexity due to outcomes with more than 2 levels. In such cases it can be difficult to determine an 'order' to the outcomes.
Log-linear models can be used for analysis of this type of data. For example, if we have some distribution where πij represents the probability that the ith individual falls under the jth category. Assuming the response categories are mutually exclusive: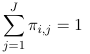
For each individual i; That is the probabilities add up to 1 for each individual, so we only have J - 1 probability parameters.
Multinomial Distribution
This is an extension of the binomial distribution involving joint distributions. Specifically each trial can result in any of the k events (E1, E2 ... Ek), each with its own respective probabilities. The probability that in n trials we observe Y1 of the E1 outcomes, y2 of the R2 outcomes ... and yk of the Rk outcomes in n independent trials is:![]()
with y1 + y1 .. + yk = n and the probabilities summing to 1
The multinomial term: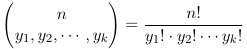
represents the number of possible divisions of n distinct objects into k distinct groups of sizes y1, y2... yk
Consider an example with k = 3 (three possible outcomes):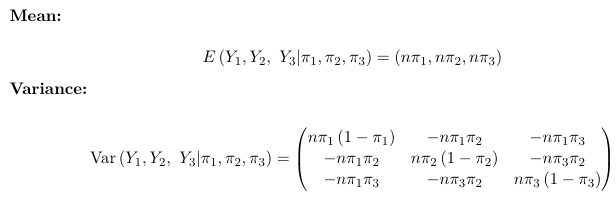
The multinomial distribution model counts are negatively correlated; The dispersion parameter is φ = 1
The binomial distribution can be thought of as a particular case of the multinomial distribution with k = 2. We want models for the mean of the response or equivalently for the probabilities, where the probabilities depend on a vector of covariates.
Link Function - Generalized Logits
Perhaps the simplest approach to the Multinomial regression is to designate one of the response categories as the reference category and calculate the log-odds for all other categories relative to the reference. For the binomial example, the reference cell is often the 'non-event' category.
So for a multinomial with J categories there are J - 1 distinct odds. For example, in a case with 3 response categories we could use the last category as the reference and hence get 2 generalized odds also called generalized logits: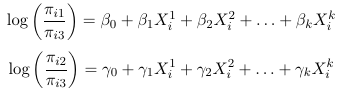
This is kind of like running 2 separate logistic regressions and estimating two separate sets of parameters, but it is a single model and all parameters are estimated by the MLE.
We can solve for the probabilities as a function of the slope parameters (beta and gamma):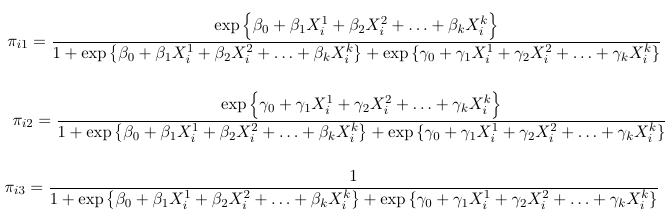
Thus, for a multinomial response with J categories, the J - 1 generalized logits are: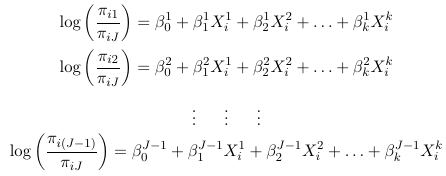
And then maximum likelihood can be used to estimate all parameters. For the intercept and each predictor, we will be estimating J - 1 parameters.

