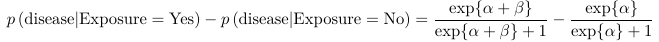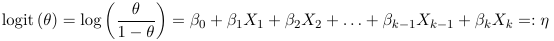Binomial Outcomes

Frequently dichotomous outcomes are used in medical studies, such as presence of a disease or exposure to some factor. The classical model does not apply outcomes that are not continuous, and many other reasons:

1. The variance of the dichotomous response is not constant
2. One could predict probabilities > 1 or smaller than 0
3. Limited interpretation of parameters

In this section we will observe alternatives to traditional linear regression for binomial data.

Generalized Linear Model For Binomial Data

• The outcome is distributed either Bernoulli or Binomial with probability of success θ
• Link function is logit and relates to the probability of success θ to the linear predictor η = β0 +β1 X1 +
  β2X2 + · · · + βk−1Xk−1 + βk Xk as follows:
  

  

• Variance function: V(θ) = θ (1 - θ)

Recall: For ordinary linear regression the distribution of outcomes is normal and the link is the identity function, and the variance is constant. For loglinear models the distribution of the outcome is Poisson, the link function is the LOG function and the variance function is the identity.

The link function is logistic because the logit function takes value between -inf to inf while the logodds is between 0 and 1.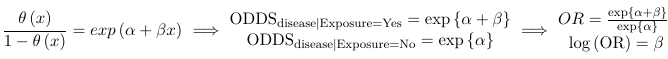

β represents the increase in logodds for a one-unit increase in X

The coefficients can also be interpreted as probability (risk) difference. However, the change is a function of base probability: