Modeling the Mean and Covariance
Suppose we have a model of mean response as a product of time on a continuous value: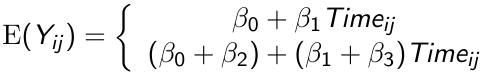
The top is control and bottom is treatment. By allowing an index for the jth measurement we allow participants to have measurement in unequal time periods.
Consider the 3 hypotheses which could be tested:
- H0: β3 = 0 for testing parallelism between groups
- H0: β1 = 0 for testing flatness of change over time
- H0: β2 = 0 for testing differences between groups
Quadratic Trends
Higher order terms should be tested (and removed from the model if appropriate) before the lower order terms
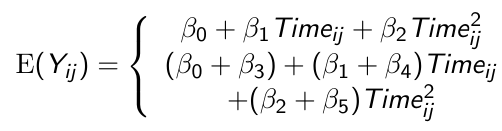
In the above we would first test β2 = 0 and if this fails to be rejected we can remove the term and test β1 = 0
To avoid potential problems with collinearity we center the variable of time around their mean before squaring it in order to include it as a quadratic term
Linear Splines
There are application in which the mean response cannot be modeled accurately using a polynomial, like when the mean response increases rapidly for some duration and then more slowly thereafter. In such a case a linear spline model would be appropriate.
Assume the mean response follows a linear trend, but the parameters change at a known time point t*; We can write the following linear spline model with a knot at time t*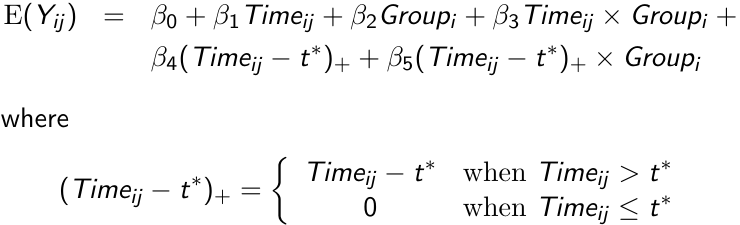
We can then write the model separately for each group before and after t*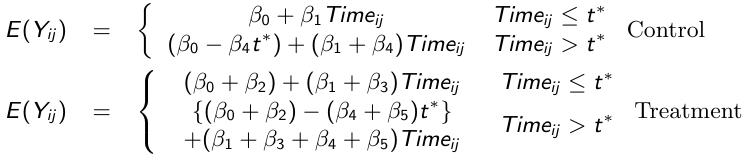
We can test the following hypotheses:
- H0: β3 = β5 = 0 for testing differences in patterns of change
- H0: β3 = 0 for testing group differences in patterns of change prior to t*
- H0: β4 = β5 = 0 for testing changes in the linear trend model after t*
