Marginal Methods
In many biomedical applications outcomes are binary, ordinal or a count. In such cases we consider extension of generalized linear models for analyzing discrete longitudinal data. These non-linear models require that a linear transformation of the mean response can be modeled in a regression setting. The non-linearity raises issues with the interpretation of the regression coefficients.
We let Yi denote the response variable for the ith subject, and: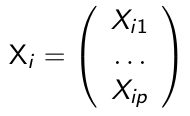
is a p*1 vector of covariates. A generalized linear model for for Yi needs the following three-part specification:
1. A Distributional Assumption
Generalized linear models assume that the response variable has a probability distribution belonging to the exponential family (normal, bernoulli, binomial or Poisson). A feature of the exponential family is the variance can be expressed as:![]()
Where phi is a dispersion parameter and v(μi) is the variance function. For example:
- Variance function of normal distribution: v(μ) = 1
- Variance function of Bernoulli: v(μ) = μ(1 - μ)
2. A Link Function
The link function g(.) applies to the mean and then links the covariates to the transformed mean η such that:![]()
For example, the canonical link functions for some common distributions are: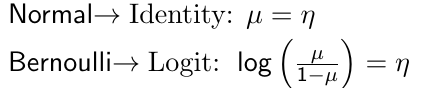
3. A Systematic Component
The systematic component specifies the effects of the covariates Xi on the mean of Yi can be expressed in terms of the following linear predictor:![]()
Note that the term 'linear' refers to the regression parameters.
Binary response
Let Yi denote a binary response variable with two categories such as presence or absence of a disease. The probability distribution is Bernoulli with Pr(Yi = 1) = μi and Pr(Yi = 0) = (1 - μi). Using the logit as the link function we have:![]()
Where μi / (1 - μi) are the odds of success
A unit change of Xik changes the odds of success multiplicitively by a factor of exp(βk).
The logistic regression model can be derived from the notion of a latent variable model. Suppose that Li is a latent continuous variable which follows a standard logistic distribution (0, π2/3) and that a positive response is observed only when Li exceeds some threshold τ , such that:![]()
It can be shown that: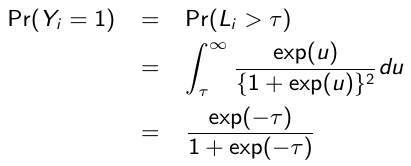
Marginal Models
Suppose Y'i = (Yi1, Yi2 ..., Yip), a vector of correlated responses from the ith subject. To analyze such correlated data we must specify or make assumptions about the multivariate or joint distribution, and to do so we will consider these main extensions of GLM: Marginal Models and Mixed Effects Models (next lecture)
A marginal model for longitudinal data has the following three-part specification:
- E(Yij | Xij) = μij is assumed to depend on the covariates through a known link function:
- We also identify a known variance function:
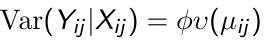
Where phi is a scale parameter that may be constant or may vary at each measurement occasion. - The conditional within-subject association among the response measurements, given the covariates, is assumed to be a function of an additional set of association parameters, α.
Note that the systematic component is the key building block of a marginal model and specifies the model for the mean response at each occasion, E(Yij | Xij), and its dependence on the covariates. Marginal responses also assume that the conditional mean of the jth response given Xi1, ..., Xin depends only on Xij:![]()
With time-invariant or fixed time-varying covariates this assumption holds. It does not hold when a time-varying covariate varies randomly over time.
Note on association: We avoid using the term correlation. This is because 1) correlation is not a natural measure of within-subject association for discrete responses, and 2) the joint distribution of discrete responses is not often well specified or not easily tractable.
SAS Code
libname S857 'C:\Users\yorghos\Dropbox\Courses\BS857\2021\Datasets';
proc logistic data=s857.BPD plots=EFFECT descending;
class BPD;
model BPD=Weight;
title1 'Simple Logistic Regression using PROC LOGISTIC';
run;
proc genmod data=s857.BPD descending;
class BPD;
model BPD=Weight/DIST=binomial LINK=LOGit;
title1 'Simple Logistic Regression using PROC GENMOD';
run;
proc logistic data=s857.BPD plots=EFFECT descending;
class BPD;
model BPD=Weight Gest_Age Toxemia;
title1 'Multiple Logistic Regression using PROC LOGISTIC';
run;
proc genmod data=s857.BPD descending;
class BPD;
model BPD=Weight Gest_Age Toxemia/DIST=BINOMIAL LINK=LOGIT;
title1 'Multiple Logistic Regression using PROC GENMOD';
run;
title1 'Marginal Logistic Regression Model for Obesity';
title2 'Muscatine Coronary Risk Factor Study';
proc freq data=s857.muscatine;
where occasion=2;
by gender;
tables age*y;
run;
data muscatine;
set s857.muscatine;
cage=age - 12;
cage2=cage*cage;
cage3=cage2*cage;
run;
/*using a compound symmetry structure working correlation*/
proc genmod data=muscatine ;
class id occasion;
model y(event='1')=gender cage cage2 / dist=bin link=logit
type3 wald;
repeated subject=id / type=cs corrw covb;
run;
/*Using Log OR correlation structure*/
proc genmod data=muscatine ;
class id occasion;
model y(event='1')=gender cage cage2 / dist=bin link=logit
type3 wald;
repeated subject=id / withinsubject=occasion logor=fullclust;
run;
/*Equivalent model*/
proc genmod data=muscatine descending;
class id occasion;
model y=gender cage cage2 / dist=bin link=logit
type3 wald;
repeated subject=id / withinsubject=occasion
logor=zrep( (1 2) 1 0 0,
(1 3) 0 1 0,
(2 3) 0 0 1) ;
run;
/*The same association between any two occasions */
proc genmod data=muscatine descending;
class id occasion;
model y=gender cage cage2 / dist=bin link=logit
type3 wald;
repeated subject=id / withinsubject=occasion
logor=zrep( (1 2) 1 ,
(1 3) 1 ,
(2 3) 1 );
run;
/*Testing whether the association between occasions 1-2
and 2-3 are the same */
proc genmod data=muscatine descending;
class id occasion;
model y=gender cage cage2 / dist=bin link=logit
type3 wald;
repeated subject=id / withinsubject=occasion
logor=zrep( (1 2) 1 0 0,
(1 3) 0 1 0,
(2 3) 1 0 1) ;
run;
/*Fitting a model with the association between occasions 1-2
and 2-3 are the same */
proc genmod data=muscatine descending;
class id occasion;
model y=gender cage cage2 / dist=bin link=logit
type3 wald;
repeated subject=id / withinsubject=occasion
logor=zrep( (1 2) 1 0 ,
(1 3) 0 1,
(2 3) 1 0);
store p1;
run;
ods graphics on;
ods html style=journal;
proc plm source=p1;
score data = muscatine out=pred /ilink;
run;
proc sort data = pred;
by gender age;
run;
proc sgplot data = pred;
series x = age y = predicted /group=gender;
run;
ods graphics off;
/*Cubic Model*/
proc genmod data=muscatine descending;
class id occasion;
model y=gender cage cage2 cage3/ dist=bin link=logit
type3 wald;
repeated subject=id / withinsubject=occasion
logor=zrep( (1 2) 1 0,
(1 3) 0 1,
(2 3) 1 0);
store p1;
run;
ods graphics on;
ods html style=journal;
proc plm source=p1;
score data = muscatine out=pred /ilink;
run;
proc sort data = pred;
by gender age;
run;
proc sgplot data = pred;
series x = age y = predicted /group=gender;
run;
ods graphics off;
/* Example of a quadratic model with gender age interaction */
proc genmod data=muscatine descending;
class id occasion gender ;
model y=gender cage cage2 gender*cage gender*cage2 / dist=bin link=logit
type3 wald;
contrast 'Age X Gender Interaction' gender*cage 1 -1, gender*cage2 1 -1 /wald;
repeated subject=id / withinsubject=occasion logor=fullclust;
run;
/*********************************
Diagnostics(Optional)
*********************************/
ods graphics on;
proc genmod data=muscatine descending;
class id occasion;
model y=gender cage cage2 cage3/ dist=bin link=logit
type3 wald;
repeated subject=id / withinsubject=occasion
logor=zrep( (1 2) 1 0,
(1 3) 0 1,
(2 3) 1 0);
assess var=(cage)/resamples=10000 seed=7435865;
run;
ods graphics off;
ods rtf close;